B1-Analyse graphique
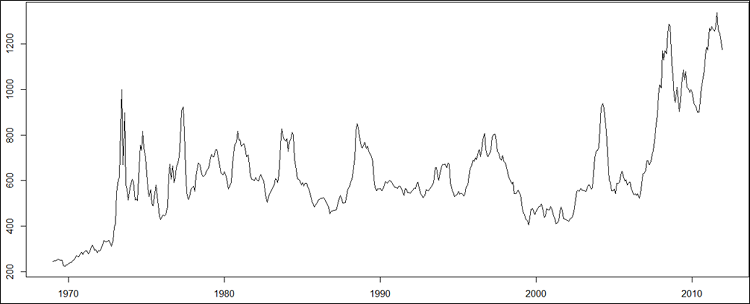
Graphe 2 :évolution du prix spot du soja de janvier 1969 à décembre 2011
Bien entendu le prix du soja est résultat de la confrontation entre l’offre et la demande. L’effet du choc pétrolier de 1973 est bien visible par le clustering de volatilité qu’il a généré, de même que ceux de la guerre du golf et de la dernière hausse brutale du prix du baril du pétrole et enfin la crise financière. La rupture de la moyenne à partir de l’année 2006 est manifeste et remet en cause la stationnarité, au même titre que la volatilité qui semble plus grande au fil du temps.
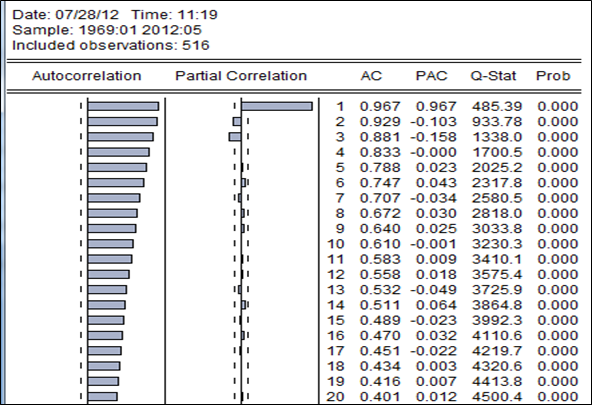
B2-Analyse du corrélogramme.
Les prix mensuels d’un mois à l’autre sont corrélés significativement dans l’ensemble. Le prix du soja possède une tendance. Les trois premiers pic de la fonction d’auto corrélation partielle est significatif, cela nous conduit à une intuition de saisonnalité dans la mesure où le soja est soumis cycles naturels qui sont sans doute la semence et la moisson.
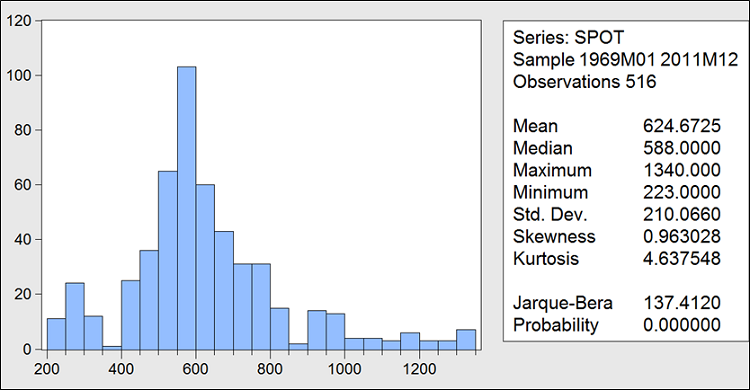
B3-Analyse de l’histogramme.
Le prix du soja n’obtempère pas à une loi normale. En moyenne le prix du soja de 1969 à 2011 tourne autour de 624,6725, le prix maximum est de 1340 et le prix min 223 soit une différence de 500%. On enregistre une asymétrie positive avec un skewness supérieur à celui de la distribution théorique de la loi normale ;ce qui indique une forte augmentation des prix par rapport à la moyenne avec une fréquence limitée, qui est bonne nouvelle pour l’agent qui souhaite une augmentation des prix.
B-4 Analyse de la variance et Test de Buys-Ballot du prix au comptant du soja
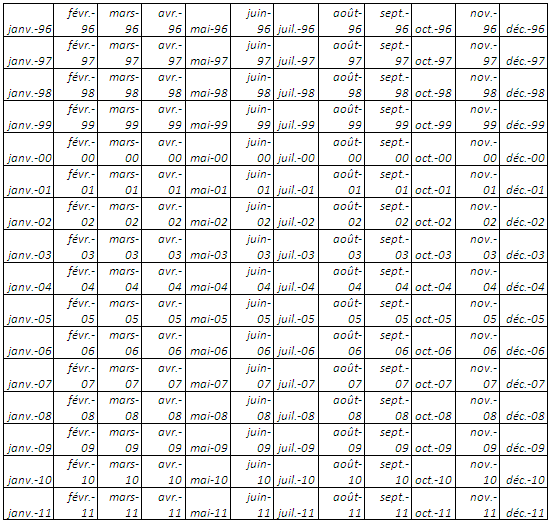
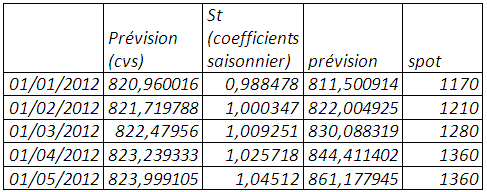
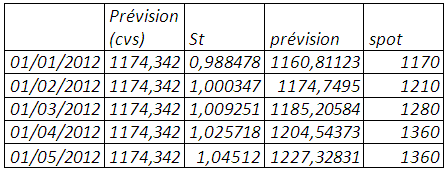
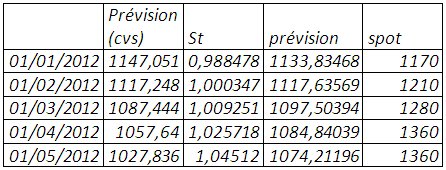
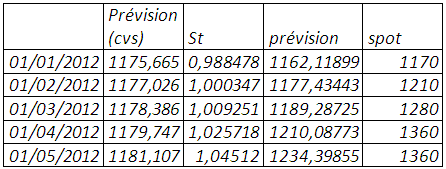
Le classement, par ordre croissant des prix pour chaque année de janvier 1969 à décembre 2011, montre à partir de janvier 1996 à décembre 2011 des creux représentés par les mois de janvier et des pics par les mois de décembre, le mois de janvier qui renvoie à l’effet « janvier » aux états unis. En effet, les années 90 ont été le théâtre de recommandations par diététiciens et scientifiques de la consommation du soja par ses propriétés nutritionnelles et thérapeutiques. Mais cette saisonnalité ne peut être confirmée que si on n’élimine la tendance si pour autant elle existe au regard du corrélogramme. De 1969 à 1995, la saisonnalité si elle existe n’est pas répétitive et bien marquée.
Tableau 1 : classement par ordre croissant des prix pour chaque année de janvier 1969 à décembre 2011
Le test de buys-ballot de janvier 1969 à décembre 2011 confirme la présence d’une saisonnalité et tendance même après élimination de la tendance. Mais cependant « désaisonnaliser » le prix du soja de 1969 à 1995 au même titre que celui de la période janvier 1996 à décembre 2011 peut introduire un biais susceptible de compromettre la prévision. Ce pourquoi nous scindons la série temporelle en deux parties et réitérons les tests de détection de saisonnalité.
Les résultats montrent que la saisonnalité provient de la période janvier 1996 à décembre 2011 qui est dissuadée par la tendance. Une dessaisonalisation « moyenne mobile » selon un schéma sans doute additif a été envisagée pour cette même période suivie d’un second test de saisonnalité qui confirme l’absence de saisonnalité et la présence de tendance sur la nouvelle chronique modifiée du prix du soja (confère annexe).
B-5 Prévision de la série par les méthodes traditionnelles
La prévision du prix anticipé du soja, en suggérant la normalité de ce dernier, montre que la tendance n’est pas déterministe même si elle est significative à peine, en plus de l’auto-corrélation et hétéroscédasticité qui conduisent à sous-estimer les valeurs futures. Le lissage exponentiel simple et celui de Holtwinters possèdent une qualité prédictive meilleure avec des erreurs moindres, ce qui n’est pas étonnant en considérant que la tendance n’est pas déterministe.
Tendance déterministe :
Lissage exponentiel simple : mse=46,34915
Lissage exponentiel double : mse=48,24433
Holwinter : mse=44,20251
B-6 Test d’efficience du marché physique du soja
Bien entendu au même titre que le marché à terme, nous testons l’efficience du marché physique au sens de l’hypothèse faible. Les prix établis résultent de l’offre et de la demande. L’étude de l’indépendance du prix vis-à-vis du temps est identique à vérifier l’efficience du marché.
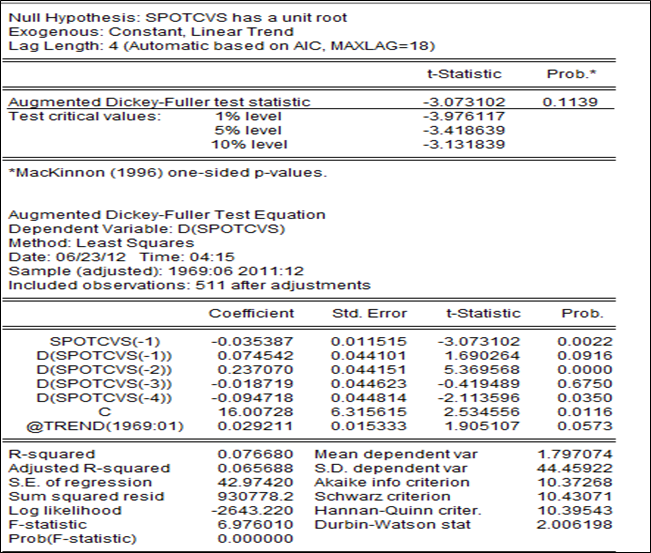
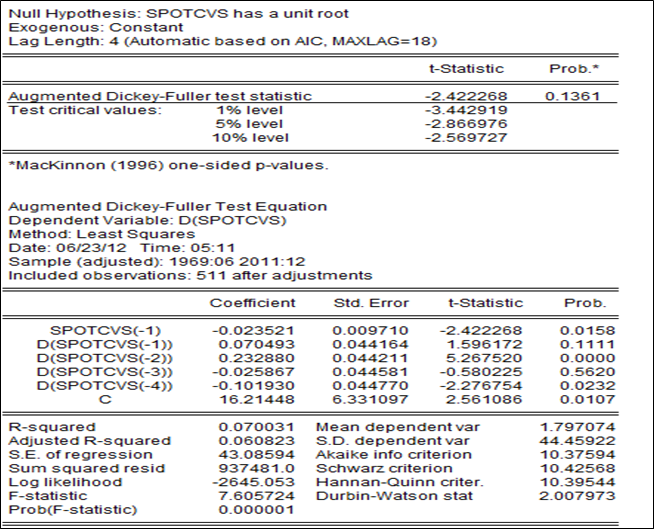
Estimation du modèle 3 :
Le prix possède pas une racine unitaire au regard de la statistique -3.07 > -3.418639 et simultanément la tendance n’est pas significative dont la statistique est inférieure à sa valeur critique lue dans la table ADF (1,90
La constante est significative au regard de sa t-statistique supérieure à la valeur critique (3.17>2.52). Le prix spot du soja suit une marche au hasard avec dérive.
〖SPOTCVS〗_t=C+〖SPOTCVS〗_(t-1)+ε_(t ) avec ε_(t )censé se comporter comme un bruit blanc iid. Ce processus est rendu stationnaire par différence première en générant la série qui est le rendement logarithmique :
〖SPOTCVS〗_t 〖-SPOTCVS〗_(t-1)=Δ 〖SPOTCVS〗_t 〖=ε〗_t +C
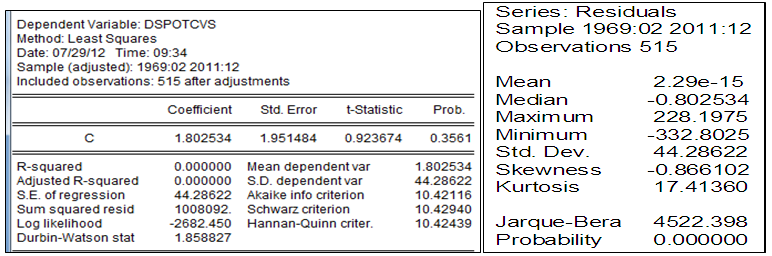
On s’aperçoit que l’hypothèse d’efficience du marché se recentre autour des variations du prix ou rendements qui sont censées être expliquées par une constante et que les erreurs, qui en découlent, suivant une loi normale, et non corrélées et homoscédastiques.
Les rendements sont loin d’être expliqués par une constante. Les erreurs, de moyenne nulle, et étalées vers la gauche confirment davantage le risque de baisse de prix auquel le producteur est exposé conjugué avec l’occurrence de prix extrêmes. Les variations de prix ne sont pas indépendantes ni normalement distribuées. Les variations de prix peuvent être expliquées par les variations et erreurs passées via les processus autorégressifs moyenne mobile. Le processus de prix spot du soja est une « marche au hasard » avec dérive à erreur.
B-7 l’approche par les modèles arma(2,2)
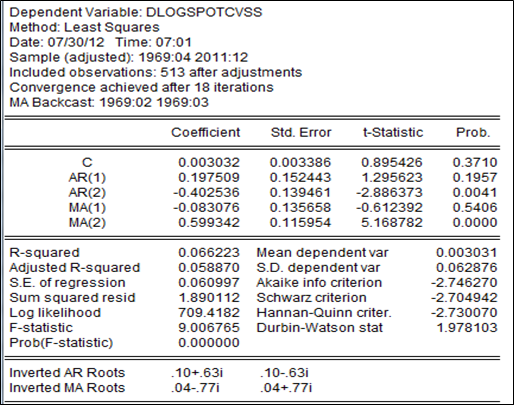
Après sélection, le rendement du prix du soja peut être représenté par le processus arma suivant :
〖∆logSPOTCVS〗_t=0.00303 +0.1975∆log〖SPOTCVS〗_(t-1)-0.4025〖∆logSPOTCVS〗_(t-2)-0.0830ε_(t-1)+0.5993ε_(t-2)
L’arma(2,2) avec constante explique pour 6,6% la variation du prix du soja, et estime que la variation retardée de deux mois ainsi que l’erreur expliquent mieux la variation actuelle que la dernière variation de prix. Ceci suppose l’existence d’une mémoire plus ou moins longue dans le processus de variation du prix du soja. Comme dans le cas du prix anticipé, les erreurs sont non corrélées, hétéroscédastiques et caractérisées par une « queue épaisse ». Cela ne nous dissuade pas de faire une prévision compte tenu de la validité qui est compromise par la non normalité et l’hétéroscédasticité.
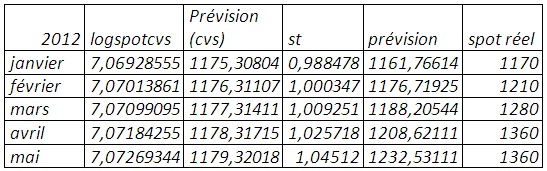
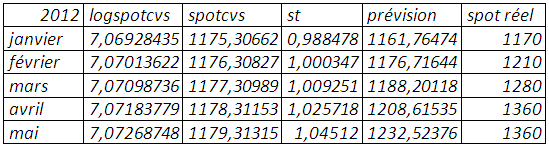
Prévision (mse=0,062815)
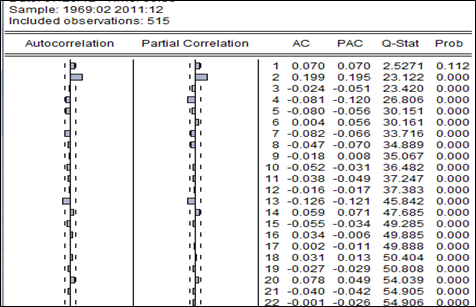
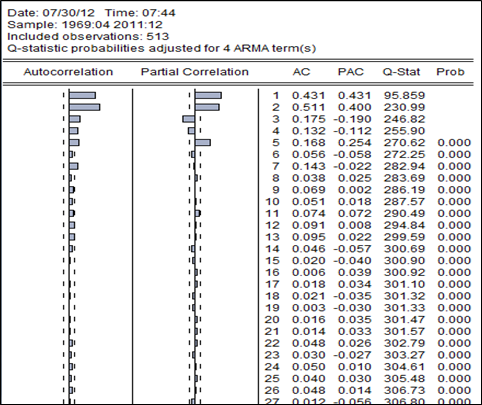
Bien entendu, la variance n’est pas constante dans le temps, le corrélogramme des résidus au carré ainsi que le test ARCH confirment l’hétéroscédasticité et l’effet ARCH.
B-8 l’approche par les modèles ARCH linéaires et non linéaires
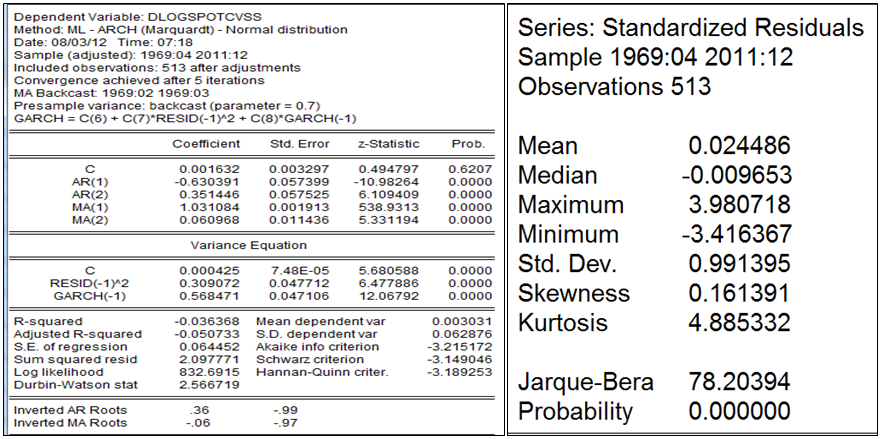
Parmi les modèles arch. linéaires et non linéaires, le garch(1,1) s’adapte mieux aux variations de prix du soja. En effet on a non auto-corrélation et homoscédasticité des résidus (cf annexe). Mais ces mêmes résidus ne suivent pas une loi normale et sont caractérisés une queue épaisse.
Ne tenant compte des signes des chocs sur la volatilité, le garch traite mieux l’épaisseur de queue quand bien même que l’Egarch et les autres arch linéaires et non-linéaire. En effet peut-on dire que l’évolution future des variations du prix mensuel du soja est fonction plus des ampleurs des chocs que de leurs signes passés. Le garch(1,1) prend mieux en compte l’occurrence faible des grandes variations du prix du soja dans le futur. Enfin le prix du soja peut être approximé à processus Arima (2,1,2) à erreur Garch.
Prévision (mse=0,062701)
la prévision de la volatilité future est donnée par l’équation de la variance :
〖∆logSPOTCVS〗_t=0.00163-0.6303∆log〖SPOTCVS〗_(t-1)+0.3514〖∆logSPOTCVS〗_(t-2)+1.031ε_(t-1)+0.0609ε_(t-2)
la prévision de la volatilité future est donnée par l’équation de la variance :
σ_t^2= 0.00042+ 0.3090ε_(t-1)^2+0.5684 σ_(t-1)^2
σ_t^2=0.00270985
La baisse du prix du soja qui ne sera pas atteinte au seuil 1% à l’horizon d’un mois ou du mois de janvier 2012 est de -12,12%.
conclusion
En somme, le prix au comptant du soja est un processus autorégressif moyenne mobile arima(2,1,2) à erreur egarch(1,1), et ce au seuil de 5%. L’hypothèse d’efficience à défaut du marché physique réel est acceptée au seuil de 5%,10% et 1%, avec une constante près de la marche au hasard en acceptant comme significatif le changement de moyenne intervenu autour années 90.
Page suivante : Section 3 Analyse multi-variée prix spot et prix future du soja
Retour au menu : La couverture des produits agricoles sur les marchés à terme : Cas du soja