A1-Analyse graphique
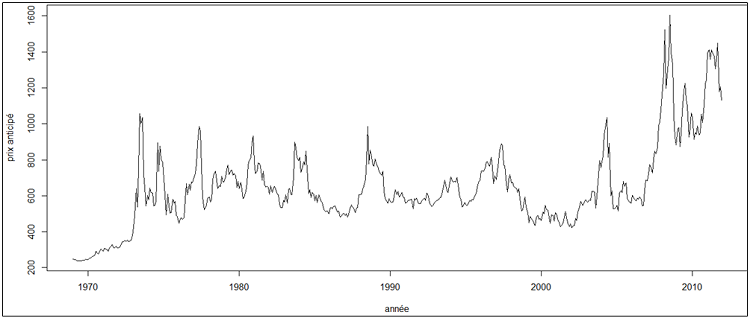
Graphe 1 :évolution du prix anticipé du soja de janvier 1969 à décembre 2011
Le graphique laisse voire une constance de la moyenne et de la variation du prix, et une indépendance vis-à-vis du temps de janvier 1969 jusqu’en 2006, année à laquelle on peut observer à « l’œil nu » un début de rupture de la moyenne conjuguée par une variation forte qui coïncide avec la crise financière de 2007 et qui se poursuit jusqu’en avril 2012. Ce début de rupture à la moyenne peut dissuader la stationnarité présumée de 1969 à 2006, et doit-on la tester. D’autre part l’évolution du prix est marquée par des pics et des creux qui semblent fréquent au regard du graphique, ce qui ne nous empêche pas de procéder à une analyse de la variance pour détecter une éventuelle saisonnalité.
A2-Analyse du corrélogramme.
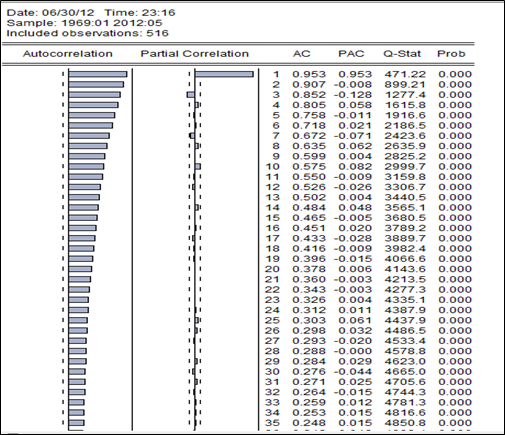
Corrélogramme du prix anticipé du soja de janvier 1969 à décembre 2011
Les coefficients d’auto-corrélation sont significatifs. En effet les prix mensuels du soja anticipés sur le marché à terme ne sont pas indépendants ; et cela rime bien avec certains « faits stylisés » comme la « prophétie auto-réalisatrice », une forte hausse est souvent suivie par une baisse et vice-versa.
La décroissance lente de la fonction d’auto-corrélation simple montre que le prix possède une tendance soit rigide ou souple. Seul le premier pic de la fonction d’auto corrélation partielle est significatif, cela nous conduit à contredire l’intuition de saisonnalité, de même la significativité continue des coefficients d’auto-corrélation laisse douter de la stationnarité.
A3-Analyse de la normalité.
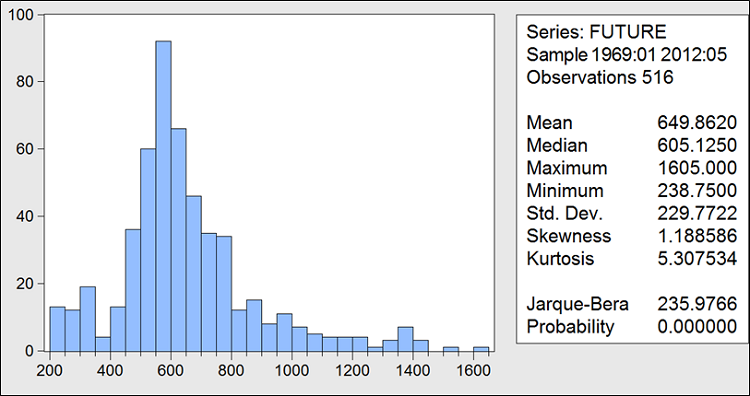
Histogramme du prix anticipé du soja de janvier 1969 à décembre 2011
En moyenne le prix anticipé du soja sur le marché à terme de 1969 à 2011 tourne autour de 649,862, le prix max est de 1605 et le prix min 238,75 soit une différence de 500%. La statistique de Jarque-Bera est largement supérieure à 5,99 pour dire que les prix « future » ne suivent une loi normale. En effet d’une part, il y a une occurrence faible de prix 1600, 1400, 1200,1000 qui s’écartent trop de la moyenne qui se situe à 649,862 caractérisant une « queue épaisse » et enregistrée par la kurtosis qui dépasse celle de la loi normale.
D’autre part, ces mêmes prix et ceux qui s’éloignent moins de la moyenne sont inégalement répartis par rapport à cette même moyenne du prix. Ce qui caractérise l’asymétrie de la distribution et est enregistrée par la skewness qui est supérieure à celles de la loi normale qui est de zéro.
A-4 Analyse de la variance et Test de Buys-Ballot du prix anticipé du soja
Le classement, par ordre croissant des prix pour chaque année, montre à partir de janvier 1996 à décembre 2011 des creux représentés par les mois de janvier et des pics par les mois de décembre. En effet, les années 90 ont été le théâtre de recommandations par diététiciens et scientifiques de la consommation du soja par ses propriétés nutritionnelles et thérapeutiques. Mais cette saisonnalité ne peut être confirmée que si on n’élimine la tendance si pour autant elle existe au regard du corrélogramme. De 1969 à 1995, la saisonnalité si elle existe n’est pas répétitive et bien marquée. Le test de Buys-ballot réalisé montre plutôt la présence d’une tendance qu’une saisonnalité. (confère annexe1)
A-5 Prévision de la série par les méthodes traditionnelles
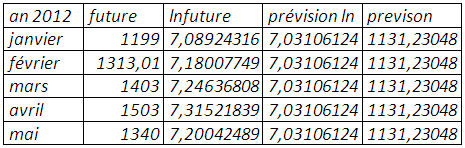
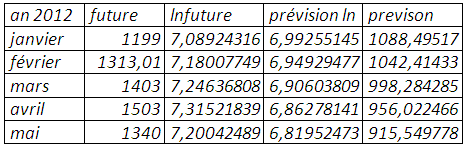
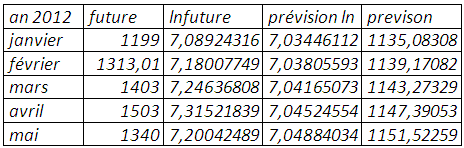
La prévision du prix anticipé du soja, en suggérant la normalité de ce dernier, montre que la tendance n’est pas déterministe même si elle est significative à peine en plus de l’auto-corrélation qui conduit à sous-estimer les valeurs futures. Le lissage exponentiel simple et celui de Holtwinters possèdent une qualité prédictive meilleure avec des erreurs moindres, ce qui n’est pas étonnant en considérant que la tendance n’est pas déterministe.
Modèle linéaire simple :
Lissage exponentiel simple :
Lissage exponentiel double :
Holtwinters :
A-6 Test d’efficience du marché à terme du soja
L’étude de l’efficience du marché à terme consiste à vérifier l’hypothèse de « marche au hasard » du prix anticipé, qui en effet englobe toutes les définitions de l’efficience du marché. Littéralement cela reviendrait à dire que le prix actuel courant anticipé pour le soja est équivalent à 100% du prix passé à défaut avec des erreurs de moyenne nulle et non corrélées de variance constante et suivant une loi normale. Le prix couvre toute l’information passée et présente, le processus du prix a une propriété de martingale. Le dernier cours passé est le meilleur « prédicateur » des valeurs futures des cours.
Autrement dit en s’intéressant à l’hypothèse faible d’efficience, il importe d’évaluer la dépendance entre les accroissements des prix et les accroissements passés et simultanément la dépendance vis-à-vis du temps.
Plusieurs études ont essayé de tester l’hypothèse de l’efficience des marchés des actifs. Pour tester la forme faible de l’hypothèse, on a utilisé l’analyse des séries temporelles en testant spécifiquement l’hypothèse d’une marche au hasard. Plus spécifiquement ces tests servent à détecter si les accroissements des prix sont indépendants des accroissements passés. Si l’hypothèse d’une marche au hasard est rejetée, alors le marché n’est pas efficient, car les accroissements de prix passés pourraient aider à anticiper les prix futur des actifs.
Le prix « future » est stationnaire de second ordre si sa variance est finie, son espérance est constante et indépendante du temps de même que la variance. Cela est identique à :
∀t∈ Z, E (〖logfuture〗_t^2)<∞
∀t∈ Z, E (〖logfuture〗_t)=m indépendant de t
∀(t,h) ∈ Z^2, cov (〖logfuture〗_t,〖logfuture〗_(t+h))=E [(〖logfuture〗_(t+h)-m)( 〖logfuture〗_t-m)]=γ(h) , indépendant de t
Le fait qu’un processus soit stationnaire ou non conditionne le choix de la modélisation que l’on doit adopter.Si l’on retient la méthodologie de BOX-JENKINS,si la série étudiée est issue d’un processus stationnaire, on cherche alors le meilleur modèle parmi la classe des processus stationnaires pour la représenter et puis on estime ce modèle.En revanche si la série est issue d’un processus non stationnaire, on doit chercher à la « staionnariser » trouver une transformation stationnaire de ce processus.Puis on modélise et l’on estime et estime les paramètres associés à la composante stationnaire.
Gra ̂ce aux deux auteurs Nelson et Plosser,les cas de non-stationnarité les plus fréquents sont analysés à partir de deux types de processus : TS trend stationary qui correspond à une non-stationnarité de type déterministe ,et DS differency stationary une non-stationnarité de type aléatoire ou stochastique.
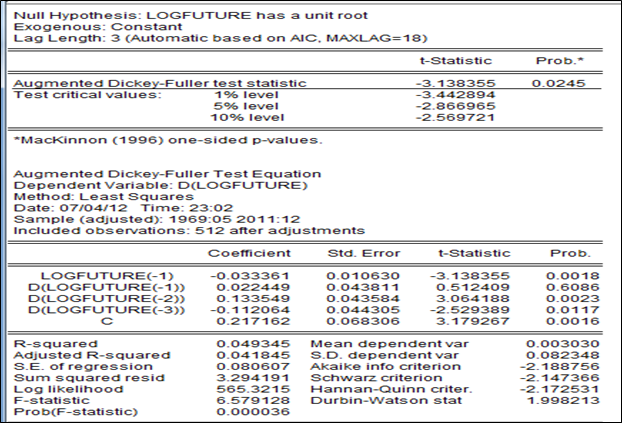
L’analyse graphique soupçonne une stationnarité mais cela ne nous empe ̂che de procéder aux tests de racines unitaires dont le plus classique est celui de Dickley Fuller. Mais en particulier le test de Philips-Perron semblera plus pertinent du fait de l’hétéroscédastité.
Le test de DF permet de déceler la stationnarité ou non d’une série par la détermination d’une tendance déterministe ou stochastique. Cependant le test DF simple suppose que l’erreur est non corrélée, ce qui est restrictif. D’où la nécessité de faire appel au test DF augmenté (ADF) qui prend en compte cet aspect de l’erreur.
On part des 3 modèles principaux sur lesquels reposent les tests.
[4] :∆X_t=ρX_(t-1)-∑_2^P▒ϕ_j ΔX_(t-j+1)+a_t
[5] : ∆X_t=ρX_(t-1)-∑_2^P▒ϕ_j ΔX_(t-j+1)+C+a_t
[6] : ∆X_t=ρX_(t-1)-∑_2^P▒ϕ_j ΔX_(t-j+1)+C+βt+a_t avec a_t~iid(0,σ_a^2)
Si l’hypothèse ρ=1 est acceptée dans l’un des 3 modèles alors notre chronique possède une racine unitaire autrement-dit elle est stationnaire.
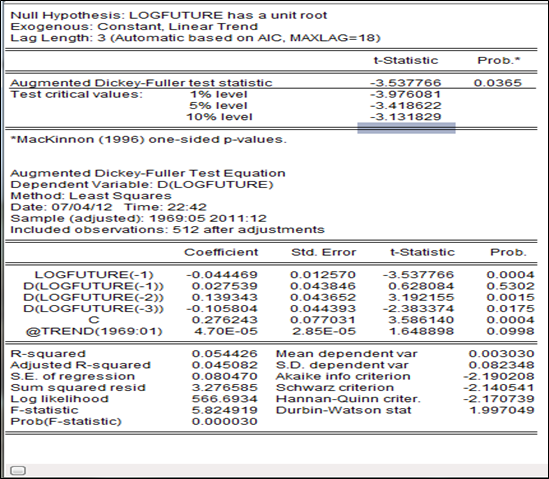
Pour les tests on opte pour la stratégie descendante en commençant par le modèle 3.L’estimation du modèle 3 donne la sortie suivante :
[6] : ∆X_t=ρX_(t-1)-∑_2^P▒ϕ_j ΔX_(t-j+1)+C+βt+a_t
Avec X_t=〖logfuture〗_t. (confère annexe le test)
Le prix anticipé ne possède pas une racine unitaire au regard de la statistique -3.537766 < -3.418622 et simultanément la tendance n’est pas significative dont la statistique est inférieure à sa valeur critique lue dans la table ADF (1,64
La constante est significative au regard de sa t-statistique supérieure à la valeur critique (3.17>2.52).
A l’issue de ce test, il semble que le prix anticipé sur le marché à terme est un processus autorégressif d’ordre 1 suivi d’une constante, ordre qui est confirmé par la fonction d’auto-corrélation partielle :
Au seuil de 5%, le prix anticipé sur le marché à terme est stationnaire et suit un processus autorégressif avec constante :
〖logfuture〗_t=〖C+ϕlogfuture〗_(t-1)+ε_(t )
La stationnarité du prix anticipé au seuil de 5% peut laisser supposer les évènements du choc pétrolier, de la crise financière comme des effets « arch » (confère supra).
L’hypothèse d’efficience sur le marché à terme dans le cas du soja. Il existe un biais. Et par conséquent les accroissements des prix ne sont indépendants des accroissements passés. Les accroissements de prix passés pourraient aider à anticiper les prix futurs. Les erreurs issue de l’explication du prix courant par le dernier prix passé sont interdépendantes (hétéroscédastiques), ne suivent la loi normale et sont caractérisées par une « queue épaisse ». Ces mêmes erreurs peuvent servir à anticiper les prix futurs. D’où l’intérêt pour les processus autorégressifs et moyenne mobile.
A-7 l’approche par les modèles arma
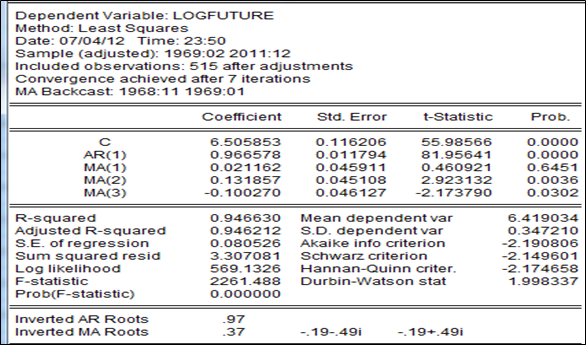
Le prix anticipé du soja sur le marché à terme peut être approché à défaut par le processus autorégressif et moyenne mobile arma(1,3) qui satisfait au mieux les critères classiques de qualités prévisionnelles (confère annexe).
Le prix peut être réécrit de la façon suivante :
〖logfuture〗_t=〖6,505+0,966578logfuture〗_(t-1)+0,021161ε_(t-1)+0,131856ε_(t-2 )-0,100269ε_(t-3 )
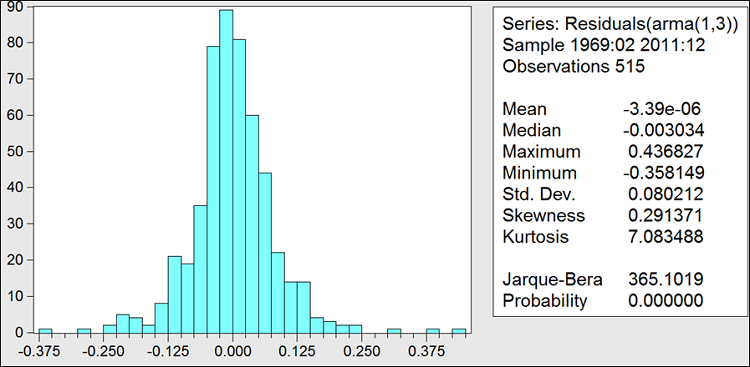
La variabilité du prix « future » du soja est expliquée pour 94% par l’arma(1,3). Les erreurs issues de cette tentative approximation du prix par ce processus arma sont de moyenne nulles et non corrélées, et caractérisées par une « queue épaisse » étalée vers la droite par conséquent ne sont pas normalement distribuées.
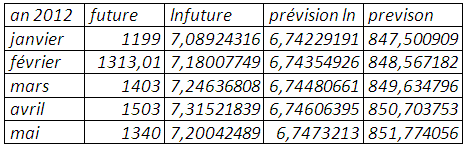
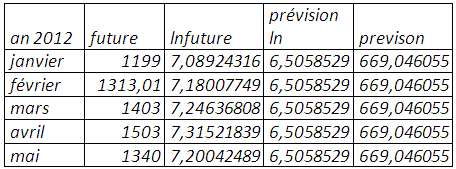
La prévision par ce modèle donne les résultats suivants :
Avec un mse de 0,272967
Les modèles arma supposent la constance de la volatilité dans le temps et une possible variation de l’espérance conditionnelle.
soit notre processus de prix :
〖logfuture〗_t=〖C+ϕlogfuture〗_(t-1)+ε_(t )
La moyenne et la variance inconditionnelles s’écrivent :
〖E[logfuture〗_t]=C/(1-ϕ)
〖Var[logfuture〗_t]=(σ_ε^2)/(1-ϕ^2 )
La moyenne conditionnelle est identique à 〖E[logfuture〗_t/〖logfuture〗_(t-1)]=〖C+ϕlogfuture〗_(t-1)+ε_(t ) dépend de l’information présente en t-1 et n’est pas nécessairement constante. Mais la variance conditionnelle reste constante. En effet :
〖Var[logfuture〗_t/〖logfuture〗_(t-1)]=〖E{〖(logfuture〗_t-〖E[logfuture〗_t/〖logfuture〗_(t-1)]²)/logfuture〗_(t-1)}
=E[〖ε_(t )〗^2/〖logfuture〗_(t-1) ]=E[〖ε_(t )〗^2 ]=σ_ε^2
La constance de la volatilité du prix anticipé face à l’arrivée de nouvelles informations est en effet irréaliste, et cela est confirmé par l’héroscédasticité qui découle du corrélogramme des résidus au carré. D’où l’intérêt de s’intéresser aux modèles Arch qui prennent en compte l’épaisseur de queue à la fois la non-constance de la volatilité.
A-8 l’approche par les modèles Arch
Les modèles Arch vont permettre de tenir compte de l’occurrence faible de prix « extrêmes » et de leur écart par rapport à la moyenne sur le marché à terme.
A-8-1 l’approche par les modèles Arch linéaires Arch(2)
Robert Engle est le premier à proposer une modélisation de séries stationnaires financières caractérisées par le phénomène de leptokurtose et la variabilité de la volatilité dans le temps. En effet la variance est une combinaison des p dernières perturbations observées élevées au carré 〖ε_(t )〗^2 avec une constante positive ce qui assure positivité de la variance : c’est le processus Arch(p) dont le moment conditionnel d’ordre 1 est nul et le second variable dans le temps.
〖σ_(t )〗^2=〖〖 ω +∑_(i=1)^p▒α_i ε〗_(t-i )〗^2
Avec ε_(t )~N(0,σ_(t ))
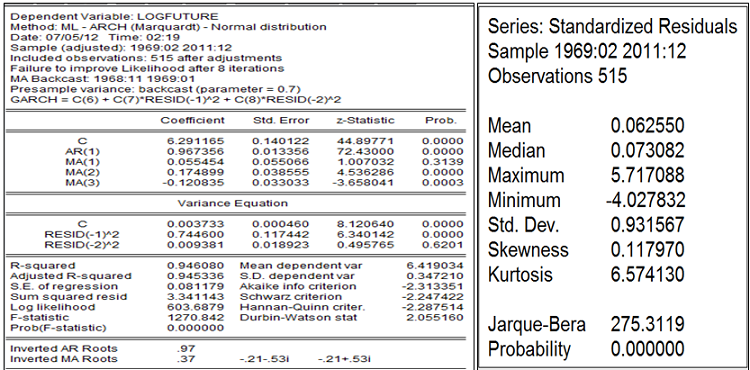
Les paramètres sont estimés par maximum de vraissamblance sous Eviews, et l’ordre p est donné par la FAP du corrélogramme du résidu au carré. Après sélection, l’arch(2) semble plus pertinent (confère annexe)
Avec l’arch(2) on a une amélioration de la normalité, avec un blanchissement du résidu et une amélioration de l’hétéroscédasticité.
La volatilité est bien sensible au dernier choc et non à l’avant dernier. A l’inverse l’erreur retardée d’un mois n’est pas significative contrairement à deux mois. L’épaisseur de queue caractérisant la distribution tendrait à sous-estimer les valeurs futures du prix anticipé.
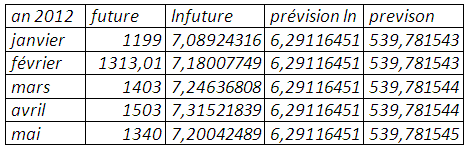
Prévision
Pour de nombreuses applications, l’introduction d’un grand nombre de retards p dans l’équation de la variance conditionnelle du modèle ARCH (p) est nécessaire pour tenir compte de la longue mémoire de la volatilité qui caractérise certaines séries monétaires et financières. Ce nombre important de paramètres peut conduire à la violation de la contrainte de non-négativité de la variance. Dans cette perspective, une extension importante, le modèle autorégressif conditionnellement hétéroscédastique généralisé (GARCH), est suggérée par Bollerslev (1986)
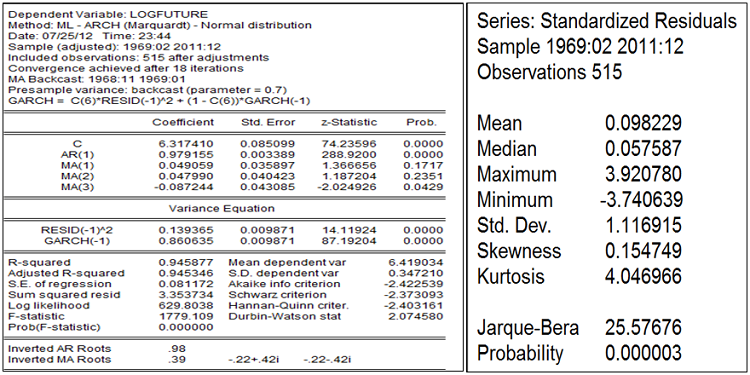
Garch(1,1)
Le processus GARCH(p,q) est une forme de modèle ARMA sur la variance conditionnelle. Cette approche exige moins de paramètres à estimer que la formulation ARCH (p) pour modéliser les phénomènes de persistance des chocs. La variance conditionnelle de la variable étudiée est déterminée par le carré des p termes d’erreur passés et des q variances conditionnelles retardées.
〖σ_(t )〗^2=〖〖 ω +∑_(i=1)^p▒α_i ε〗_(t-i )〗^2 〖〖 +∑_(i=1)^q▒β_i σ〗_(t-i )〗^2
Avec α_i et β_i≥0 ,ω>0,∑_(i=1)^p▒〖+α_i 〗 ∑_(i=1)^q▒β_i
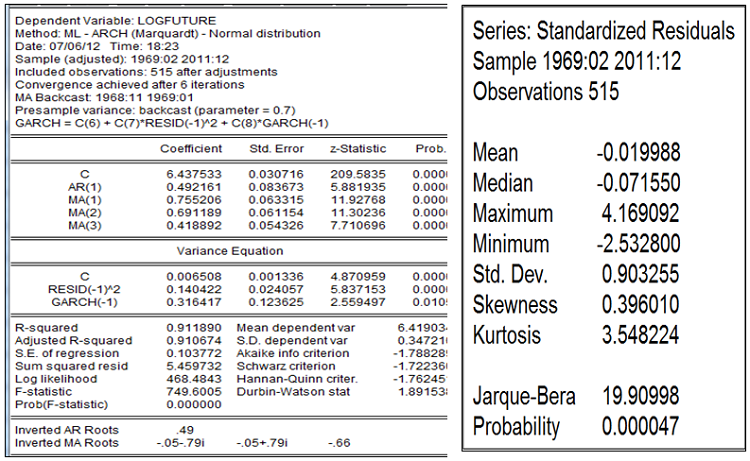
On a une très nette amélioration de la normalité, mais les résidus ne sont plus « bruit blanc » et sont hétéroscédastiques. Tous les ordres des processus autorégressifs et moyennes mobiles sont significatifs, autrement dit les contrats à terme passés expliquent davantage le présent contrat à terme.
L’effet autorégressif de la volatilité est très significatif ainsi que la sensibilité de la volatilité à la denière innovation. En effet l’ampleur des derniers chocs et volatilité jouent bien sur la future volatilité du prix anticipé. La faible épaisseur de queue dissuade à peine la prévision.
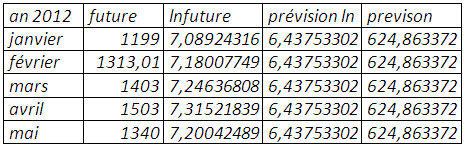
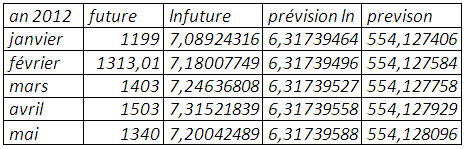
Prévision
Modèle igarch
En bref, le processus IGARCH permet une persistance infinie de la volatilité. L’effet d’un choc se répercute sur les prévisions de toutes les valeurs futures. Sa spécification est identique à un modèle GARCH (p,q) à la différence qu’une contrainte sur la somme des coefficients est imposée, elle doit être égale à 1. Ceci implique que la variance non conditionnelle n’existe pas dans ce processus.
〖σ_(t )〗^2=〖〖 ω +∑_(i=1)^p▒α_i ε〗_(t-i )〗^2 〖〖 +∑_(i=1)^q▒β_i σ〗_(t-i )〗^2
Avec α_i et β_i≥0 ,ω>0,∑_(i=1)^p▒〖+α_i 〗 ∑_(i=1)^q▒β_i =1
Appliqué au prix à terme du soja sur le marché à terme, on a :
Les résidus issus de l’igarch sont non corrélés mais sont hétéroscédastiques. L’igarch aboutit aux mêmes résultats que le garch à défaut d’une queue plus épaisse qui sous-estime les valeurs futures des prix à terme.
Prévision (mse=0,323793)
Garch-M
Quant au modèle GARCH-M, il introduit la volatilité comme un déterminant de la série stationnaire qui est, dans notre cas le prix anticipé. La variance conditionnelle est alors une variable explicative dans l’équation du prix anticipé, elle intervient dans la fonction de régression pour conditionner le prix future espéré. L’équation de la variance conditionnelle du modèle GARCH-M est identique à la formulation standard du processus GARCH, elle peut être substituée par un autre processus de volatilité.
Les résidus issus de l’igarch sont non corrélés mais sont hétéroscédastiques. L’igarch aboutit aux mêmes résultats que le garch et l’igarch à défaut d’une queue plus épaisse qui sous-estime les valeurs futures des prix à terme et de l’influence singulière et significative du dernier contrat à terme. Ceci peut être rapproché à l’efficience du marché de près.
Prévision (mse=0,268994)
Dans l’ensemble, les modèles linéaires reposent sur une spécification quadratique des perturbations sur la variance conditionnelle. Ils supposent que l’ampleur et non pas le signe des chocs qui détermine la volatilité. Par conséquent, les chocs positifs et négatifs de même taille ont un impact identique sur la variance conditionnelle. En d’autres termes, ce sont des processus symétriques. Pourtant, l’hypothèse d’effet asymétrique des chocs sur la volatilité, à savoir la variance conditionnelle réagit différemment aux chocs de même amplitude selon le signe de ces derniers, est très réaliste pour des séries financières et monétaires. Les modèles ARCH symétriques ont le désavantage de ne pas tenir compte de ce fait stylisé possible dans les séries étudiées.
A-8-2 l’approche par les modèles Arch non linéaires
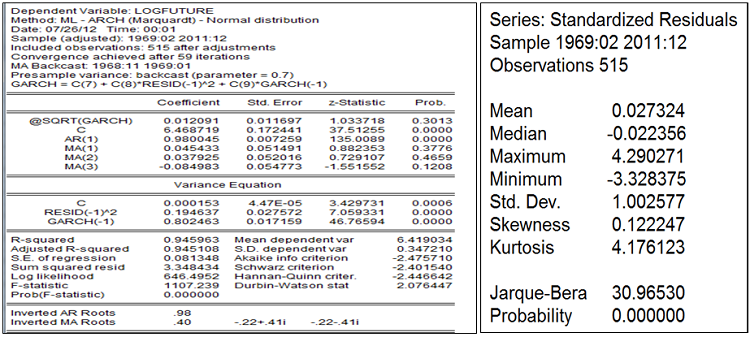
Egarch(3,2)
Sur les marchés un choc négatif a un effet plus prononcé sur la volatilité qu’un choc positif. Nelson en 1991 propose l’EGARCH qui est l’exponentiel GARCH qui lève en même temps la restriction sur les paramètres.
〖lnσ〗_t^2=w+β〖lnσ〗_(t-1)^2+α|ε_(t-1)/σ_(t-1) |+γ ε_(t-1)/σ_(t-1)
Dans le cas du modèle EGARCH, il est inutile d’imposer des contraintes sur les paramètres pour satisfaire la condition de positivité de la variance conditionnelle en raison de son écriture logarithmique.
Le paramètre α permet de modéliser un effet asymétrique lié au signe de l’innovation. Si α > 0 (respectivement si α < 0), un choc positif sur la variance conditionnelle à la date t se traduira à la date t+1 par une augmentation (respectivement une diminution) de la variance conditionnelle, c’est-à-dire de la volatilité. Le paramètre γ permet de prendre en compte une asymétrie liée à l’amplitude de l’innovation. Si γ = 0, alors une innovation positive aura le même effet (en valeur absolue) sur la variance conditionnelle qu’une innovation négative. En revanche, si γ > 0 un choc de forte d’amplitude aura relativement plus d’effet (en valeur absolue) sur la variance conditionnelle qu’un choc de faible ampleur.
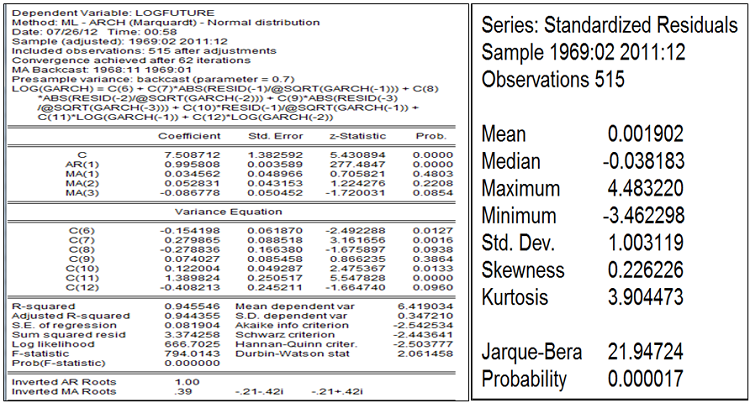
Les résidus issus de l’egarch sont non corrélés et homoscèdastiques et sont plus proches de la normalité avec une réduction considérable de l’épaisseur de queue. Les chocs négatifs ont un effet plus significatif sur la volatilité conditionnelle que les positifs. Le prix anticipé est largement expliqué par le dernier contrat à terme à 99%.
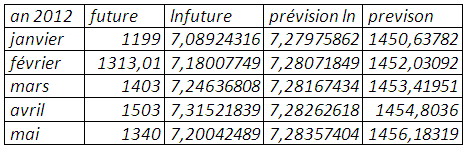
L’egarch(3,2) explique mieux le prix anticipé sur le marché à terme et la qualité de prévision meilleure. En dépit de sa qualité de suivi du prix « future » moindre que dans le cas Holtwinters, l’egarch traite mieux l’épaisseur de queue.
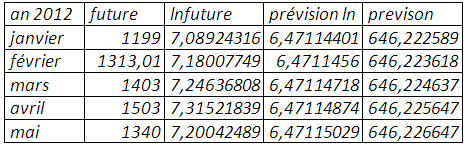
Prévision (mse=0,49809)
conclusion
En somme, le prix anticipé sur le marché terme du soja est un processus autorégressif moyenne mobile arima(1,0,3) à erreur egarch(3,2), et ce au seuil de 5%. Autrement dit l’hypothèse d’efficience à défaut du marché à terme est rejetée au seuil de 5%, mais aussi elle peut être acceptée au seuil de 1% avec une constante près de la marche au hasard en acceptant comme significatif le changement de moyenne intervenu autour années 90.
Page suivante : Section 2 : analyse uni-variée du prix spot
Retour au menu : La couverture des produits agricoles sur les marchés à terme : Cas du soja