5.1. Coefficients de mortalités
5.1.1. Coefficient de mortalité totale (Z)
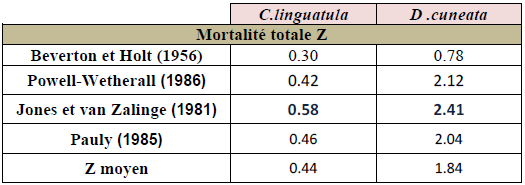
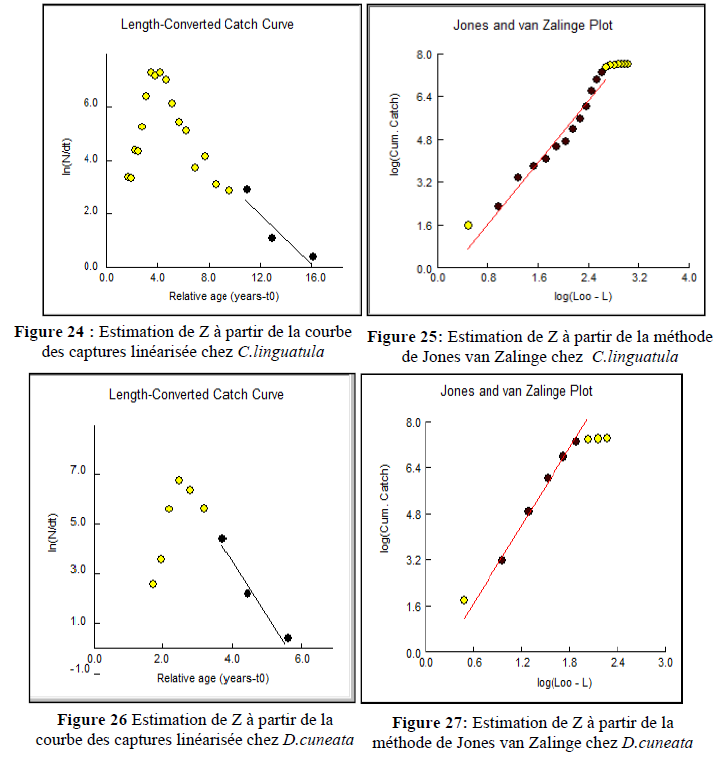
Les valeurs de Z estimées à l’aide du logiciel « FISAT II» à partir des distributions de fréquences de taille par quatre méthodes différentes, les résultats sont consignés dans le tableau 16 illustrés par les figures 24, 25, 26, 27.
Tableau 16: Estimation de coefficient instantané de mortalité totale(Z) de C. linguatula et D. cuneata selon différentes méthodes
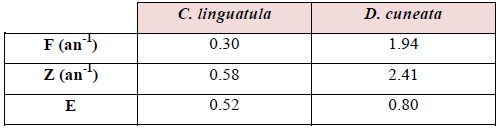
Le coefficient de mortalité totale (Z) varie entre 0.3 et 0.58 an-1 avec une valeur moyenne égale à 0.44 pour C. linguatula. Chez D. cuneata Z varie de 0.78 à 2.41 an-1 avec une valeur moyenne égale à 1.84.Les valeurs retenues sont celles de la méthode de Jones et Van Zalinge (1981) pour les deux espèces afin d’entamer l’étude de l’exploitation.
5.1.2. Coefficient de mortalité naturelle (M)
Trois relations empiriques estiment le coefficient de la mortalité naturelle, dont certaines combinent la température moyenne annuelle du milieu dans lequel vit l’espèce.
La température moyenne annuelle retenue pour cette étude est de 14°c pour C. linguatula et D. cuneata. Les résultats obtenus sont présentes dans le tableau suivant :
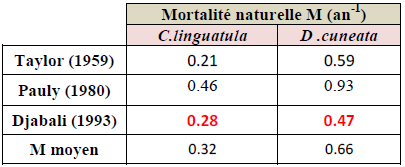
Tableau 17 : Estimation de coefficient instantané de mortalité naturelle (M) de C. linguatula et D. cuneata selon différentes méthodes
L’estimation de la mortalité (M) pour C. linguatula a aboutit à des résultats allant de 0.21 à 0.46 an-1 avec une valeur moyenne de 0.32 an-1, et de 0.47 à 0.93 an-1 avec une moyenne de 0.66 pour D. cuneata.
La valeur de M retenue pour les deux espèces est celle obtenue par la méthode de Djabali et al (1993) du fait que cette derrière se base sur des stocks méditerranéens.
5.1.3. Coefficient de mortalité par pêche (F)
Le coefficient instantané de la mortalité par pêche peut être estimé à partir de la mortalité naturelle (M) et de la mortalité totale (Z).
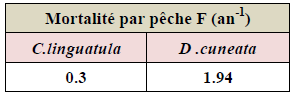
Le tableau 18 regroupe les valeurs estimées de la mortalité par pêche (F)
Tableau 18 : Estimation de coefficient instantané de mortalité par pêche (F) de C. linguatula et D. cuneata
Pour les deux espèces C. linguatula et D. cuneata les résultats estimés directement par la méthode habituelle (Z-M) sont retenus.
La mortalité par pêche (F) dépend directement des modifications de l’effort de pêche.
5.2. Le taux d’exploitation (E)
Le taux d’exploitation est estimé à partir de la mortalité par pêche (F) et de la mortalité totale (Z).
Les résultats obtenus sont consignés dans le tableau suivant :
Tableau 19 : Estimation de taux d’exploitation (E) de C. linguatula et D. cuneata
Les valeurs du taux d’exploitation indiquent un état de surexploitation pour D. cuneata, alors que pour C. linguatula cette valeur reflète une situation d’exploitation équilibrée de sa pêche, diagnostic à compléter par l’utilisation des modèles d’exploitation.
5.3. Estimation de la taille de sélection
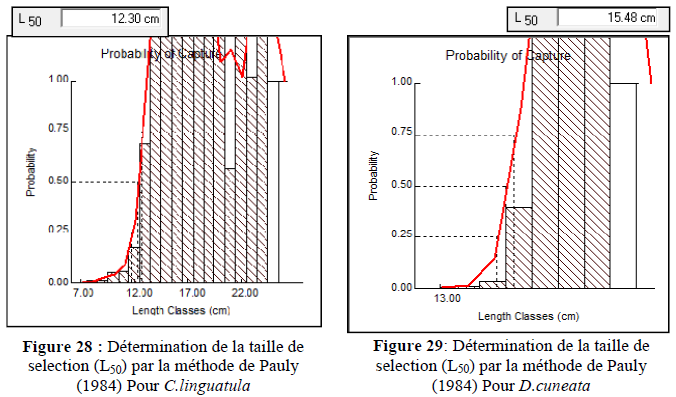
Pour l’étude de la sélectivité de l’engin de pêche, les courbes de sélection des deux espèces ont été tracées à partir des probabilités exprimées en pourcentages de capture, illustrées par les figures 28, 29.
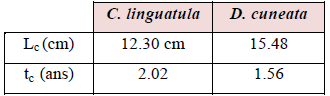
Les calculs ont été effectués à l’aide du logiciel « FISAT II ». Le tableau récapitule les résultats des tailles de sélection (Lc) :
Tableau 20 : Estimation de la taille de sélection de C. linguatula et D. cuneata
Les figures 28 et 29, représentant les variations de la probabilité (P) en fonction des centres de classe de tailles (Li), permettent d’estimer graphiquement la taille de sélection Lc, correspondant à l’abscisse au point d’ordonnée 50%. La taille moyenne de première capture déterminée ainsi est de 12.30cm pour C. linguatula pour des longueurs extrêmes allant de 8 à 27cm, elle est relative à un groupe d’âge moyen de première capture égale à 2.02 ans environ, chez D. cuneata, la taille de sélection est de 15.48cm à un âge de 1.56 ans.
5.4. Estimation du niveau d’exploitation
5.4.1. Modèle du rendement relatif par recrue : modèle de Beverton et Holt (1966)
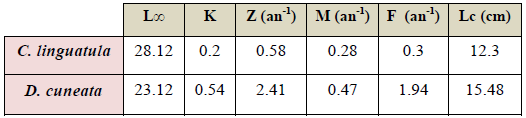
Les paramètres de croissance et d’exploitation (tableau 21) obtenus précédemment ont permis de calculer le rendement relatif par recrue Y’/R.
Tableau 21 : Paramètres de croissance et d’exploitation de C. linguatula et D. cuneata utilisés pour le calcul de Y’/R.
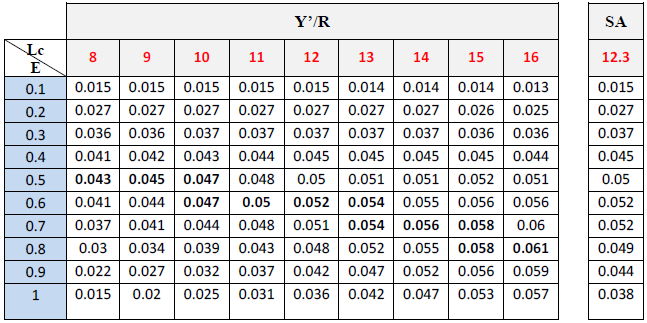
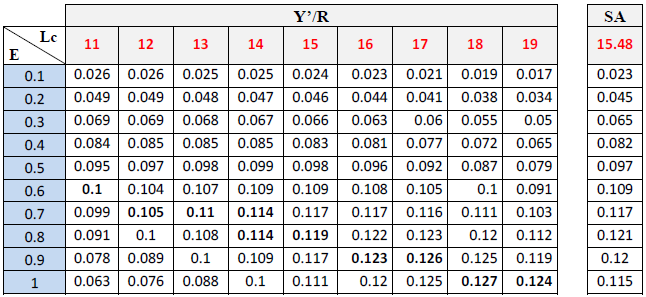
Les rendements relatifs par recrue Y’/R calculés pour différentes valeurs de E et de Lc pour C. linguatula et D. cuneata, sont reportés dans les tableaux 22, 23 et illustrés par les figures 30et 31.
Tableau 22 : Rendement relatif par recrue en fonction de E et pour différentes valeurs de Lc pour de C.linguatula
Tableau 23 : Rendement relatif par recrue en fonction de E et pour différentes valeurs de Lc pour D.cuneata
Pour les différentes tailles de première capture Lc et en fonction du taux d’exploitation E le rendement relatif par recrue Y’/R augmente jusqu’à un maximum puis il diminue.
Pour C. linguatula, à une taille de première capture de 12.30 cm, le rendement relatif par recrue actuel est à son optimum.
De même, pour D. cuneata à une taille de première capture de 15.48cm, le rendement relatif par recrue a atteint la valeur optimale.
Les valeurs du taux d’exploitation (E) qui apportent un meilleur rendement varient de 0.5 à 0.8 pour C. linguatula et de 0.7 à 0.9 pour D. cuneata. En considérant la mortalité totale Z qui est respectivement de 0.58 et 2.41, les meilleurs rendements sont obtenus à un F allant de 0.29 et 0.46 pour C. linguatula et de 1.69 à 2.17 pour D. Cuneata.
Le rendement relatif par recrue atteint son maximum (0.061g pour C. linguatula, 0.127g pour D. cuneata) pour une taille de première capture respectivement de 16 cm et 18cm.
La différence entre ce rendement relatif maximum et la situation actuelle est de 0.01 pour C. linguatula et de 0.006 pour D. cuneata.
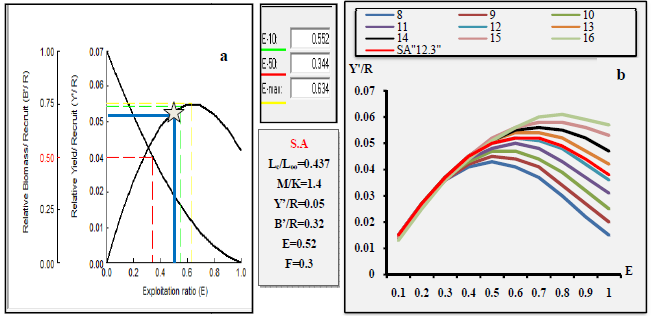
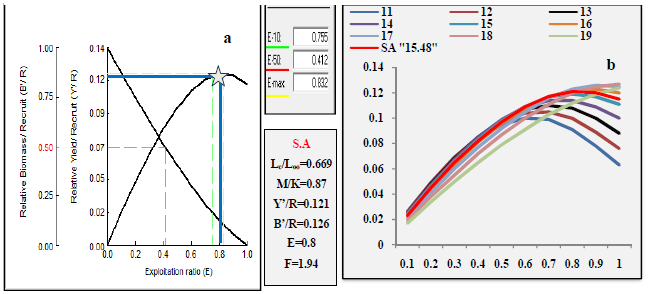
La méthode de « Knife-edge selection » du FISAT II a permis de dresser des courbes de rendement (figures 30 a et 31a) pour les rapports M/K de 1.4 et Lc/L∞ de 0.44 pour C.
linguatula ; alors que chez D. cuneata ces mêmes rapports sont de 0.87et 0.67.Cette méthode permet de déterminer le rendement relatif par recrue et la biomasse relative par recrue en fonction du taux d’exploitation (E).
Figure 30 : Rendement relatif par recrue en fonction du niveau d’exploitation pour C.linguatula
Figure 31 : Rendement relatif par recrue en fonction du niveau d’exploitation pour D.cuneata
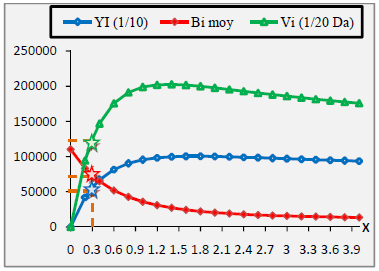
Les valeurs actuelles du rendement relatif par recrue et la biomasse relatif par recrue sont pour C. linguatula de 0.05g et de 0.32g pour un niveau d’exploitation de 0.52 relatif à un effort de pêche de 0.3. Concernant D. cuneata les valeurs du rendement et de la biomasse relatifs par recrue sont de 0.121g et 0.126 g pour un niveau d’exploitation de 0 .80 relatif à un effort de pêche de 1.94.
Le E actuel est de 0.52 pour C. linguatula. Pour ce stock l’exploitation se trouve sur la partie ascendante de la courbe, ce taux est proche du rendement optimum. Concernant D. cuneata, l’exploitation est au niveau du plateau de leur courbe correspondant ainsi à un rendement optimal car le E max reste supérieur au E actuel.
La valeur prédictive E0.1, taux d’exploitation pour une augmentation de Y’/R de C. linguatula de 1/10iéme, est de 0.552 et E0.5, valeur de E sous la quelle le stock a été réduit de 50% de sa biomasse inexploitée est de 0.344, celle correspondant à la production maximale (Emax) égal à 0.634, pour D. cuneata ces valeurs sont respectivement 0.755 ,0.412 et 0.832.
Le résultat de la situation actuelle pour les deux espèces met en évidence un rendement relatif optimal, l’exploitation des deux espèces étudiées semble être en équilibre.
Vu que le niveau optimum du rendement relatif par recrue est atteint pour les deux espèces, il sera inutile de changer le maillage du filet ainsi que l’effort de pêche.
5.4.2. Modèle de l’analyse des cohortes de Jones (1984) fondée sur la longueur
Les valeurs des paramètres utilisés pour l’étude de ce modèle et appliqués à C. linguatula et D. cuneata sont consignées dans le tableau suivant :
Tableau 24 : Paramètres utilisés pour l’analyse des cohortes de Jones (1984) fondée sur la longueur :
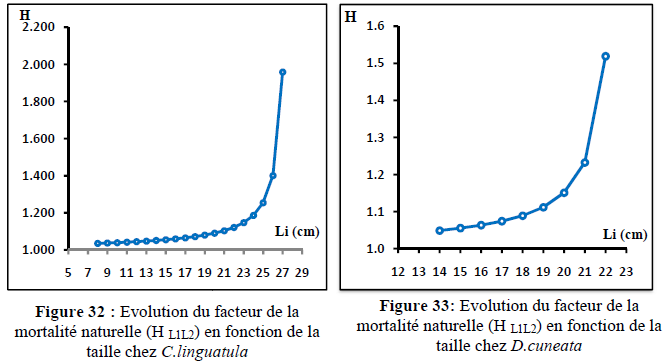
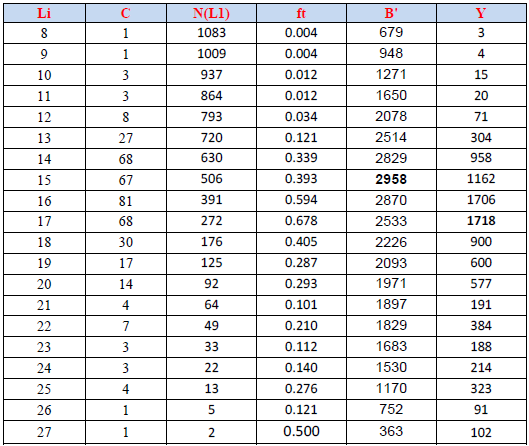
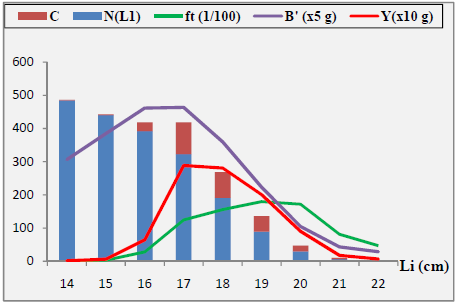
Les résultats obtenus lors de cette étude de l’analyse des cohortes de Jones (1984) fondée sur la longueur, appliquée au stock de C. linguatula et D. cuneata sont regroupés dans les tableaux 25 et 26 respectivement et 5,6(Annexe III) illustrés par les figures 32, 33,34 et 35.
L’analyse des figures 32 et 33 montrent que le coefficient de mortalité naturelle (H L1L2) augmente avec la taille.
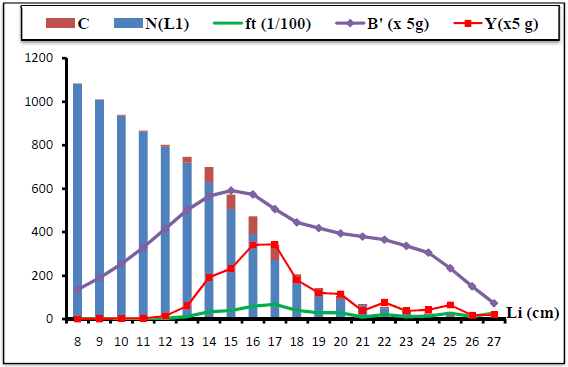
Tableau 25 : Résultats de l’analyse de cohorte de Jones (1984) fondée sur la longueur pour C. linguatula
Figure 34 : Résultats de l’analyse de cohorte de Jones (1984) fondée sur la longueur pour C. linguatula
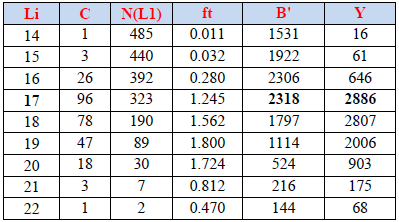
Tableau 26: Résultats de l’analyse de cohortes de Jones (1984) fondée sur la longueur pour D.cuneata
Figure 35 : Résultats de l’analyse de cohorte de Jones (1984) fondée sur la longueur pour D.cuneata
Les données de capture du stock montrent que :
– Chez C. linguatula les captures les plus importantes en nombre appartiennent à des classes de taille allant de 13à18 cm, un pic est observé à 16 cm, alors que chez D. cuneata ces captures varient de 16 à 20 cm avec un pic à 17 cm.
– L’évolution de la mortalité par pêche montre une faible pression de pêche exercée sur les juvéniles ayant des tailles inférieures à 13 cm pour C. linguatula, et inférieures à 16 cm pour D. cuneata. D’autant plus la taille de première maturité sexuelle est acquise à 19 cm pour les femelles (Garcia et al.2000) et 15 cm pour les mâles (Vassilopoulou et Papaconstantinou, 1994) chez C.linguatula, chez D.cuneata elle est de 16 cm pour les femelles et 14 cm pour les mâles (Forest, 1975), de ce fait les juvéniles restent à l’abri de toute exploitation.
– La pression de pêche augmente dans la gamme des tailles moyennes jusqu’à atteindre 0.678 an-1pour C. linguatula et 1.80 an-1pour D. cuneata.
– La biomasse moyenne (B) du stock augmente jusqu’à atteindre une valeur maximale ≈ 2958 Kg correspondant à la taille 15 cm, pour C. linguatula, et de 2318 Kg à une taille de 17 cm pour D. cuneata, puis diminue graduellement avec la taille.
Le modèle appliqué aux stocks de C. linguatula et D. cuneata fait apparaitre une diminution du stock de survivants, ceci se traduirait par une mortalité totale élevée chez les grands individus.
La courbe de production montre que le maximum (≈1718 g) chez C.linguatula et de (≈2886 g) chez D.cuneata, ces deux valeurs correspondent à 17 cm. Ces deux pics de production observé, sont probablement dues à :
– Un changement du comportement migratoire.
– La maturité sexuelle qui fait augmenter la vulnérabilité et donc la capture des espèces.
La classe de taille présentant en raison de sa biomasse importante, un intérêt économique élevé, n’a pas été convenablement ciblée, il sera préférable de diminuer la taille de capture d’une classe de taille.
5.4.3. Modèle prédictif de Thompson et Bell (1934) fondé sur la longueur :
Les valeurs des paramètres utilisés pour l’étude de ce modèle sont consignées dans le tableau suivant :
Tableau 27 : Paramètres utilisés pour le modèle de Thompson et Bell (1934).
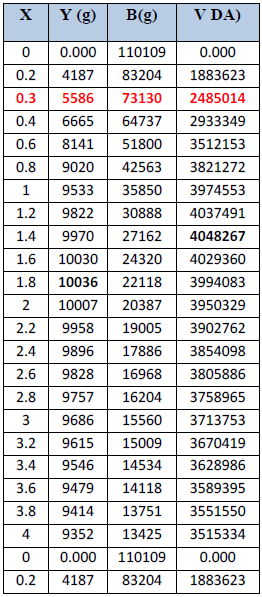
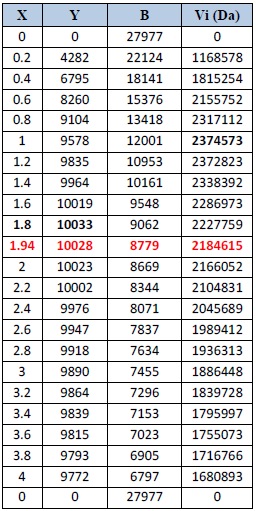
Les résultats d’application de ce modèle sur les deux espèces sont regroupés dans les tableaux 28, 29 (7, 8 en annexe V) illustrés par les figures 36 et 37.
Le modèle utilisé fait apparaître la production maximale équilibrée (MSY), la production économique maximale équilibrée (MSE), le facteur de F et la biomasse correspondante.
Tableau 28 : Résultats de l’analyse de Thompson et Bell (1934) fondée sur la longueur pour C. linguatula
Figure 36 : Evolution de la production, de sa valeur et biomasse pour différents niveaux de x pour C.linguatula
Tableau 29 : Résultats de l’analyse de Thompson et Bell (1934) fondée sur la longueur pour D.cuneata
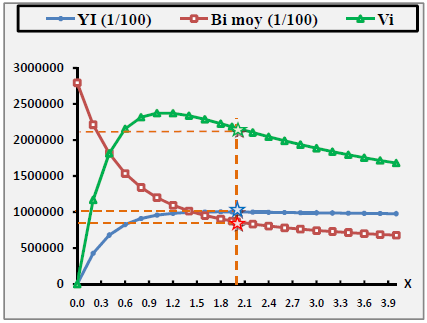
Figure 37 : Evolution de la production, de sa valeur et biomasse pour différents niveaux de x pour D.cuneata
Chez C. linguatula la production maximale équilibrée est obtenue avec un facteur de F(X=1.8) alors que la production maximale économique équilibrée est obtenue avec un facteur de F(X=1.4). Concernant D. cuneata, Le facteur de F de 1.8 correspond donc au MSY alors que le MSE est obtenu avec un facteur de F(X=1), La valeur de F actuel chez C. linguatula se trouve sur la partie ascendante de la courbe de production (Y=5586) et de la valeur (V=2485014 Da), dont la biomasse est de 73130. Les résultats montrent que le niveau présent de l’effort de pêche est inférieur à celui qui correspond au MSY et MSE pour cela il est préférable d’augmenter l’effort de pêche ; contrairement à D. cuneata où cette valeur se situe sur la partie descendante de la courbe de la valeur (V) et au niveau du plateau de la courbe de production (Y). Les résultats montrent que le niveau de l’effort de pêche est supérieur à celui qui correspond au MSE. Ceci indique que l’exploitation de ce stock dépasse son niveau optimum, pour cela et en référence à l’analyse des cohortes, il sera judicieux de diminuer l’effort de pêche et de réduire la taille de capture. Concernant C.linguatula il est préférable d’augmenter l’effort de pêche tout en ciblant des tailles moyennes.