La TVE appliquée à la Value-at-Risk permet d’évaluer le degré de résistance des variations des marchés, au même titre que le degré de solidité d’une voiture en phase de crash-test. Le comportement stochastique des extrêmes issus d’un échantillon permet la mise en place d’un cadre mathématique rigoureux.
S’intéressant directement à la queue de distribution, faisant apparaître le degré d’importance statistique des extremums, nous allons dans cette section présenter, à partir des résultats obtenus précédemment, une stratégie de gestion basée sur le calcul de la Value-at-Risk. Notre étude va porter sur la rentabilité ajustée du risque que peut proposer la VaR déterminée à partir du quantile des extrêmes sur le DJIA pendant la crise des Subprimes. En proposant une telle stratégie, un investisseur pouvait-il éviter les pertes liées à cette crise ? Pouvait-il bénéficier d’un Tracking-Error avantageux en achetant lorsque la VaRt > Rt et en vendant lorsque la VaRt < Rt au seuil de probabilité fixé ? Nous allons mettre en avant deux mesures liées à la VaR : dans un premier temps, nous sélectionnerons un modèle adéquate quant à la validité du modèle présenté, puis dans un second temps, nous calculerons, à partir des résultats obtenus, la performance que pouvait développer une stratégie long-short du 13/06/2006 au 31/12/2010.
II.II.3.1 COUVERTURE CONDITIONNELLE
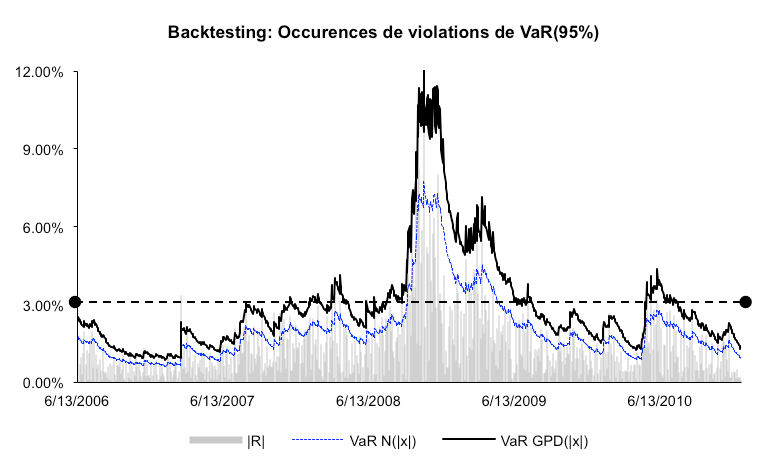
Le modèle lié à la loi normale se révèle inadapté pour estimer le risque réel. Il enregistre un taux de 9.91%, dépassant de 4.91 point le taux d’échec accepté. Cet échec est attendu dans la mesure où ce modèle de mesure du risque ne permet pas de prendre en compte le caractère leptokurtique des rendements.
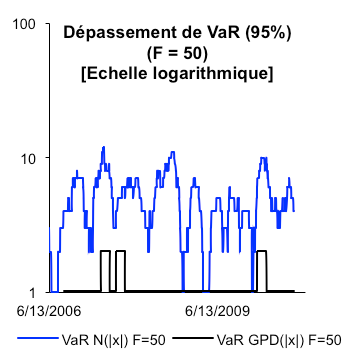
En période de crise, la VaR GPD ne laisse apparaître qu’une infinité de dépassements journaliers sur F = 50. Le ratio de couverture conditionnelle nous indique qu’il existe un taux de dépassement de 1,05% pour une Value-at-Risk acceptant 5% de risque. Ce modèle rempli donc les conditions pour un dépassement qui ne sous-estime, ni ne surestime le risque de marché. Ce modèle conditionnel fournit une quantification plus flexible de la VaR, qui tient compte de la dynamique de la volatilité. En effet, lorsque le taux de croissance dépasse le seuil u fixé à 3%, la VaR conditionnelle « vibre », couvrant le risque de perte extrême. Le graphique ci-dessous souligne la différence qu’il peut exister entre la VaR classique et celle liée aux valeurs extrêmes.
En outre, nous retenons le modèle de VaR GPD conditionnée à partir d’un seuil fixé à 3%. Nous allons, dans la sous-section suivante, établir une stratégie long-short à partir des résultats obtenus ci-dessus.
II.II.3.2 MODÈLE DE RENTABILITÉ AJUSTÉE DU RISQUE
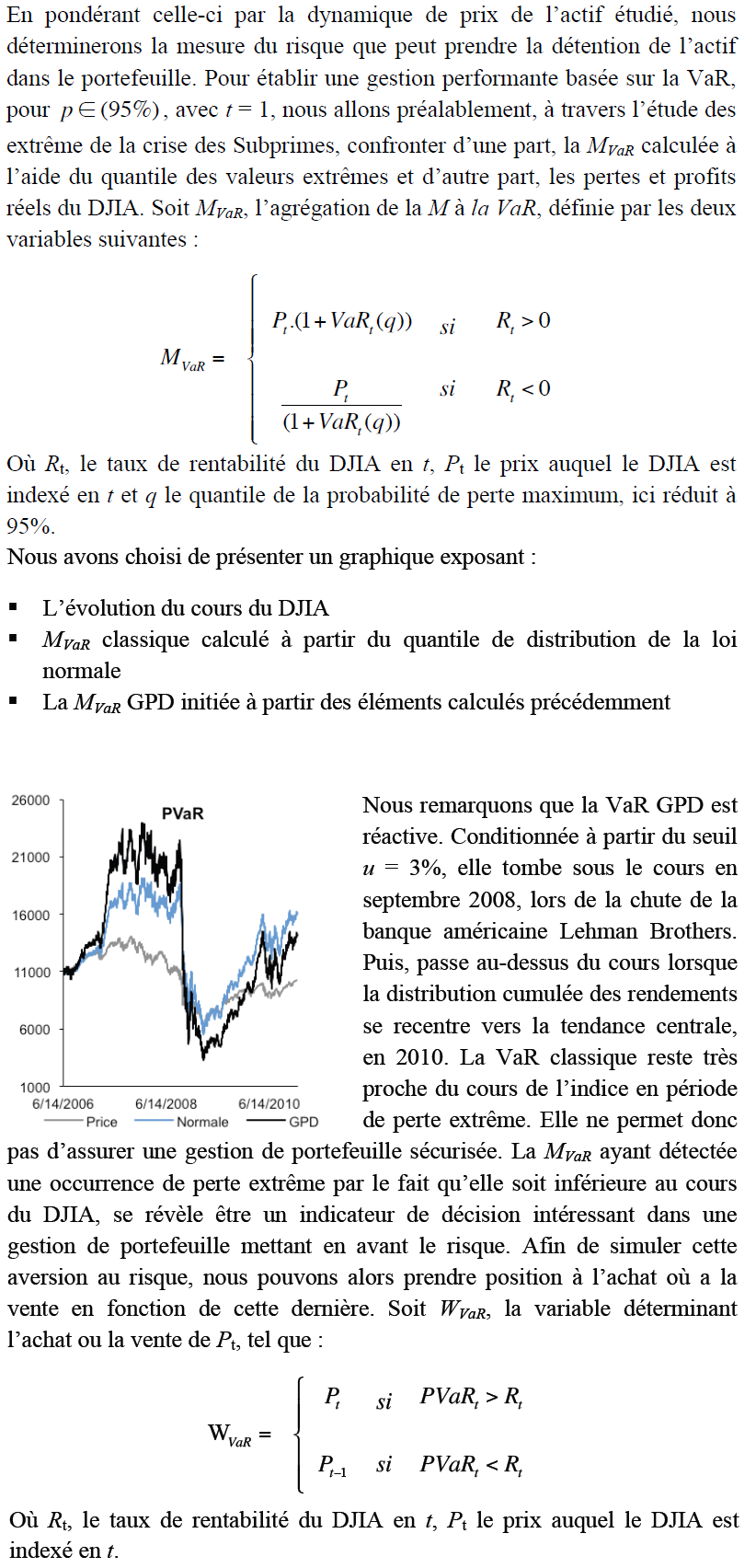
Cette sous-section montre comment la théorie des valeurs extrême peut être utilisée comme stratégie de couverture du risque de marché. Celle-ci implique la distribution asymptotique univariée des taux de rendement minimum et maximum d’une position de marché. La VaR est calculée en fonction d’une formule d’agrégation du risque, laquelle prend en compte :
– Le facteur de sensibilité des extrêmes, à travers une méthode conditionnelle
– La corrélation entre les facteurs de risque et la position du marché
Nous suivrons l’évolution de la VaR analysée à partir cette hypothèse.
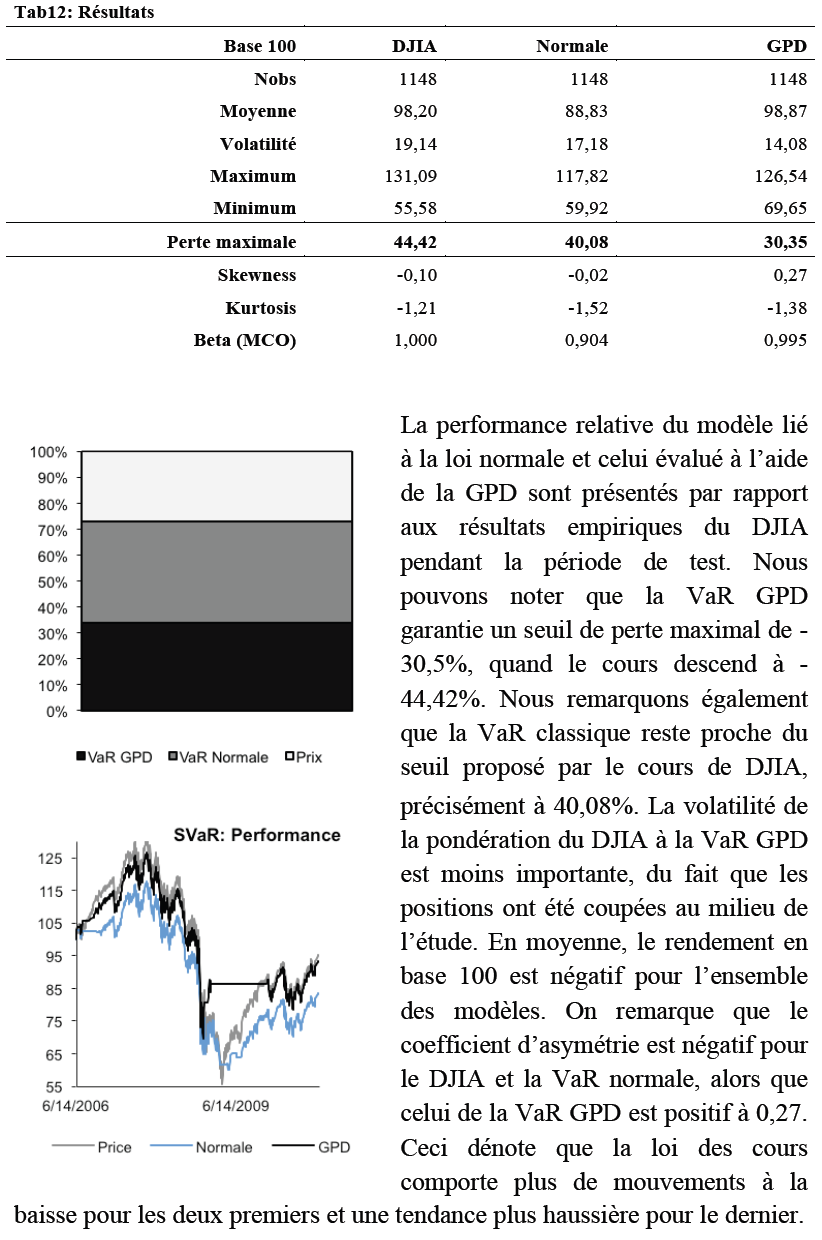
Nous présentons dans le tableau ci-dessous les résultats empiriques de notre analyse :
50 Initialement développé par Campbell S. D, en 2005.
51 En d’autres termes, 95% des variations journalières seront contrôlées avec seulement 5% d’erreur de prévision
52 Le ratio de couverture fut développé par Kupiec en 1995. Il fut ensuite repris par Christoffersen en 1998