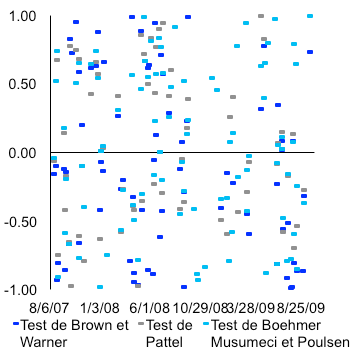
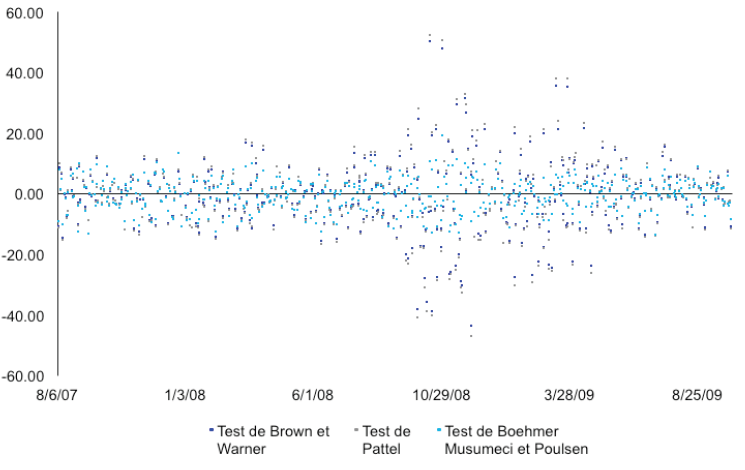
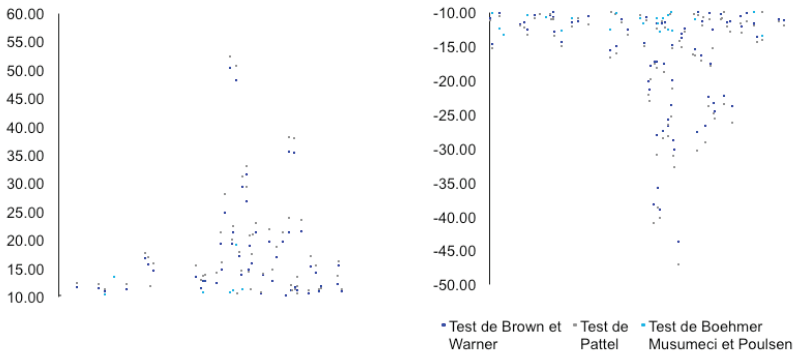
Il convient de noter par ailleurs que les trois statistiques de représentativité fournissent des conclusions globalement convergentes. Celles-ci deviennent de plus en plus significative au milieu de l’étude, autour du 3/10/2009, date à laquelle les rentabilités anormales cumulées sont les plus importantes. Il existe cependant plusieurs phases quant à la validité de ce test. Certaines valeurs semblent être plus significatives que d’autres. Les statistiques proches de 0, comprises entre [-1 ; 1], rejettent l’hypothèse d’anomalie statistique. D’autres sont, sans nul doute, incontestables au seuil de [-10 ; -50] et [10 ; 60]. Cela nous laisse penser qu’il y a des mouvements plus calmes et d’autres plus agités.
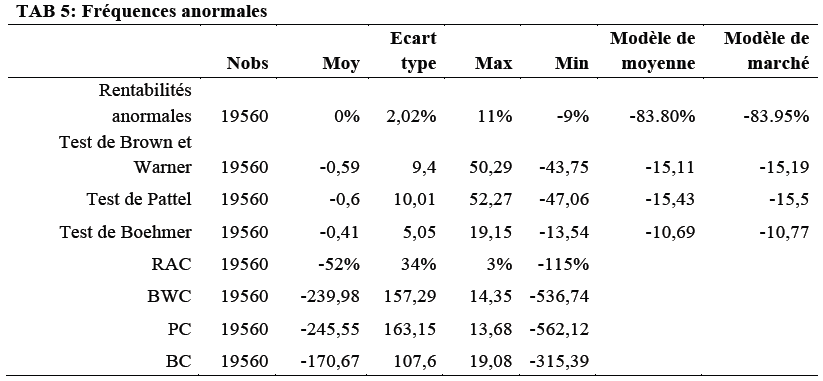
La statistique fréquentielle de Boehmer, ayant une propension plus importante à accepter l’hypothèse selon laquelle les rentabilités anormales sont nulles, est distinctement supérieure de 0, élevé à 10.69 et 10.77 en valeur absolue, respectivement pour le modèle de moyenne et celui de marché. Ce tableau résume les observations menées dans cette étude :
Ce test est par conséquent concluant dans sa globalité. Les rentabilités anormales calculées précédemment montrent l’ampleur de la crise des Subprimes et la nécessité d’instaurer une politique de mesure du risque viable. Il nous montre également qu’il existe des taux de rentabilités extrêmes dont la distribution asymptotique normale ne prévoit pas les effets.
Page suivante : II.II. THÉORIE DES VALEURS EXTRÊMES ET VALUE-AT-RISK