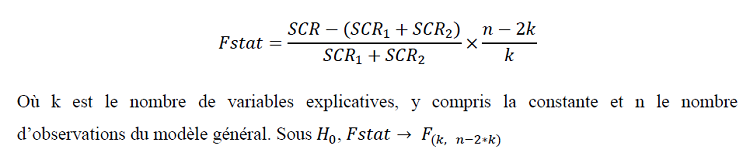Dans les études de données de panel, il apparait nécessaire de s’assurer de la spécification homogène ou hétérogène du processus générateur des données, (Doucouré, 2008). Cela revient à tester l’égalité des coefficients du modèle étudié dans la dimension individuelle. Le test de spécification permet de déterminer si le modèle théorique est parfaitement identique pour tous les pays ou s’il existe des spécificités propres à chaque pays. Ainsi, les tests de spécification se feront équation par équation afin de retenir la méthode d’estimation la plus appropriée pour l’ensemble du modèle. Ces tests de spécifications ainsi que les estimations se feront sous le logiciel stata 11. Les résultats détaillés des différents tests et régressions sont présentés en annexe n°2. Seule, la synthèse de ces résultats sera mise en exergue dans la suite du document.
a. Likelihood Ratio Test (Test de Fisher)
Les hypothèses du test sont les suivantes :
H0: Absences d’effets fixes
H1 : Présence d’effets fixes
La statistique de Fischer calculé suit sous l’hypothèse H0 une loi de Fischer. A cet effet, l’hypothèse de présence d’effets fixes ne sera pas rejetée lorsque la statistique calculée est supérieure à la valeur critique lue sur la table de Fisher. Les résultats des tests sont les suivants.
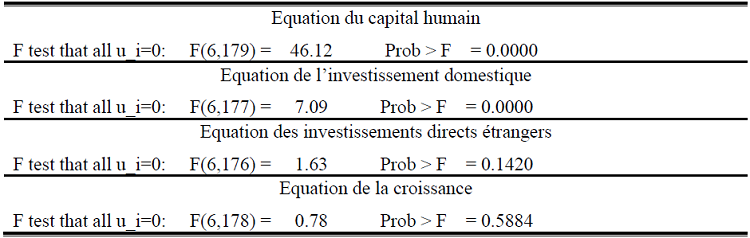
Tableau n°4 : Tableau synthétique des résultats du test de spécification de Fisher
Source : Construit à partir des résultants des différentes régressions
Pour les variables endogènes, capital humain et investissement domestique, la probabilité de la statistique de Fischer calculée est inférieure à 1%. Par conséquent l’hypothèse H0 est rejetée, et le modèle à effets fixes est plus approprié.
En revanche, la probabilité de la statistique de Fischer calculée est supérieure même au seuil de 10% pour les variables, investissements directs étrangers et croissance. Dans ce cas, l’hypothèse H0 ne peut pas être rejetée, et alors le modèle à effets fixes n’est pas approprié.
b. Test de Breusch et Pagan
La statistique de Breusch-Pagan est obtenue après l’estimation du modèle à effets aléatoires. Elle permet de tester la significativité du modèle à effets aléatoires. Si la probabilité de la statistique de Breusch-Pagan est inférieure au seuil fixé, les effets aléatoires seront globalement significatifs. Le test est basé sur les hypothèses ci-après :
H0 : Absence d’effets aléatoires
H1 : Présence d’effets aléatoires
Etant donné que le test d’identification privilégie l’estimation par les doubles moindres carrés, nous avons procédé à une estimation par les moindres carrés ordinaires en deux étapes avant d’effectuer le test de Breusch-Pagan sur la dernière estimation.
Les résultats des tests sont ainsi synthétisés dans le tableau n°5 suivant.
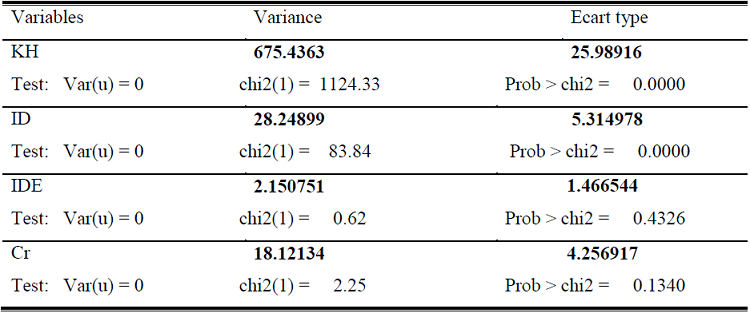
Tableau n°5 : Tableau synthétique des résultats du test de spécification de Breusch-Pagan
Source : Construit à partir des résultants des différentes régressions
Les effets aléatoires sont significatifs au seuil de 1%, pour les équations du capital humain et des investissements domestiques.
Par contre, on ne rejette pas l’hypothèse nulle d’absence d’effets aléatoires pour les deux autres équations car la probabilité de la statistique est supérieure même au seuil de 10%.
c. Test de Hausman/Hausman généralisé
Le test de Hausman permet de tester la présence d’une corrélation ou non entre les effets spécifiques et les variables explicatives du modèle. Ce qui permet de choisir entre le modèle à effets fixes et le modèle à effets aléatoires, Kpodar (2007). Le test de Hausman repose sur les hypothèses suivantes :
H0 : Il n’ya pas de différence systématique de coefficients
H1 : Il existe une différence entre les coefficients
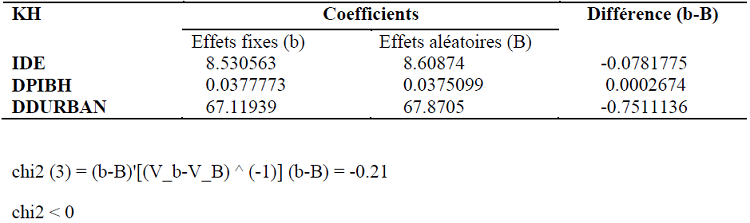
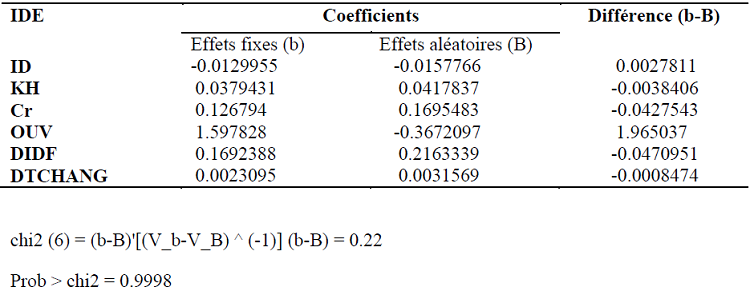
Les résultats du test de Hausman post estimation sont ainsi présentés.
Le Chi-deux est négatif, de ce fait, nous avons procédé par le test de Hausman généralisé, afin de surmonter cette contrainte. Le test de Hausman généralisé fournit les résultats ci-après.
Test de Hausman généralisé(22)
chi2 ( 2) = 3.65
Prob > chi2 = 0.1614
La probabilité de la statistique du test est supérieure à 10%. Il n’y a donc pas de différence systématique entre les deux modèles. Dans une telle situation, Kpodar (op. cit) indique le choix de l’un ou l’autre modèle doit être justifié rigoureusement, et il dépend de la conviction de chaque auteur sur la pertinence d’un modèle par rapport à l’autre. Mais Doucouré (op.cit), soutient que dans ce cas, le modèle à effets aléatoires est plus approprié que celui à effets fixes.
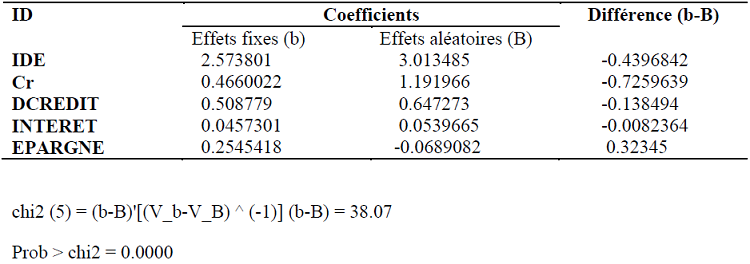
– Equation de l’investissement domestique
La probabilité du test est inférieure à 1%. Alors, le modèle à effets fixes est préférable au modèle à effets aléatoires.
– Equation des investissements directs étrangers
L’hypothèse d’absence de différence systématique de coefficients entre les deux modèles n’est donc pas être rejetée.
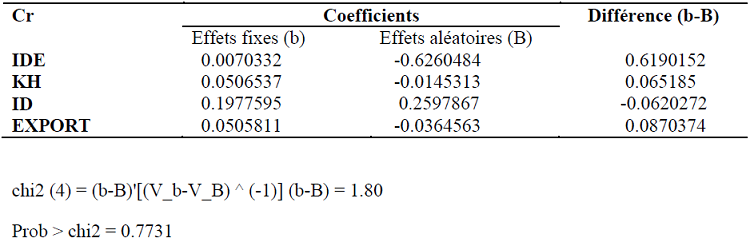
– Equation de la croissance
Ici également, l’hypothèse d’absence de différence systématique de coefficients entre les deux modèles n’est donc pas rejetée.
En somme, la prise en compte des effets spécifiques pays est appropriée pour estimer les paramètres des différentes équations du modèle. De plus, les statistiques de Wald indiquent que le modèle est globalement bien spécifié pour toutes les équations. Par ailleurs, le test de Hausman montre également qu’il n’y a pas de différence systématique entre les coefficients des deux modèles pour les équations du capital humain, de l’investissement direct étranger et de celui de la croissance. Toutefois, les coefficients de détermination issus des estimations avec les effets aléatoires montrent que la variation inter individuelle (pays) des variables est plus importante que la variation intra individuelle pour ces équations du modèle. Ainsi, le modèle à effets aléatoires est alors significatif pour ces équations.
Au regard de ces résultats, le modèle final à estimer sera un panel hétérogène à effets aléatoires pour les toutes équations, hormis l’équation des investissements domestiques qui sera estimée à effets fixes.
d. Test de stabilité du modèle
Le test de Chow ou test de changement structurel, permet de tester la stabilité des coefficients de la régression entre deux périodes ou deux sous échantillons différents. Le test de Chow temporel nous permettra de savoir si les coefficients des différentes régressions ne sont pas affectés par la dévaluation du FCFA intervenue en 1994. Le choix de cette période se justifie par le fait qu’elle correspond à une phase de profondes réformes de libéralisation dans les économies des pays membres de l’UEMOA, marquées par la mise en oeuvre des programmes d’ajustement structurel.
Le test repose sur les hypothèses suivantes :
La statistique de Chow est donnée par :
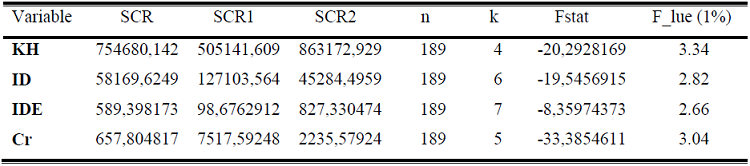
Les résultats des régressions sous stata sont ainsi présentés :
Dans toutes les équations, les statistiques calculées sont inférieures aux statistiques lues sur la table de Fischer, au seuil de 1% ; on ne peut donc pas rejeter l’hypothèse nulle de stabilité des coefficients. Par conséquent le modèle est globalement stable. De ce fait la dévaluation du FCFA n’a pas d’effet différencié sur la stabilité des coefficients du modèle.
22 Voir annexe n°3 pour les résultats détaillés du test de Hausman généralisé
Page suivante : IV. Résultats de l’estimation économétrique et interprétation des résultats