Dans ce présent chapitre, il est ignoré la saisonnalité du prix spot du soja négligeable et cachée par la tendance ainsi que les processus autorégressifs et moyennes mobiles. De surcroit, nous renouons avec l’hypothèse faible d’efficience du marché à terme à défaut en considérant le prix anticipé comme une marche au hasard avec dérive. Dans le plus de simplifier, il est retenu des représentations garch(1,1) ou à la limite des arch(1) dans l’estimation de la DCC-MVGARCH(1,1).
Ignorer le coût de l’énergie, en l’occurrence le prix du pétrole dans le processus de production et de port, semble bien restrictif dans le but de se protéger contre la variation du prix au comptant du soja. Nous considérons, en plus du prix anticipé sur le marché à terme, le prix mensuel au comptant du baril de pétrole de janvier 1969 à décembre 2011.
〖dspot〗_t=c+〖hdlogfuture〗_t+〖dlogpetrol〗_t
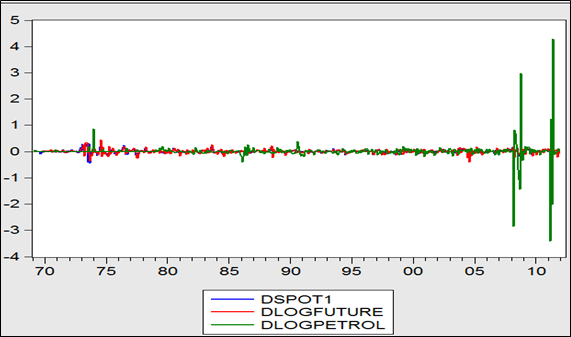
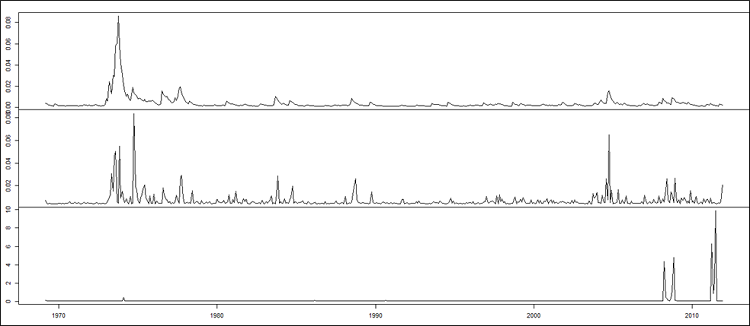
Graphe 4: variations mensuelles des prix spot et à terme du soja et des prix du baril de pétrole
1- Méthodologie
L’agent doit optimiser son portefeuille en maximisant une fonction objective qui varie positivement avec le rendement moyen du portefeuille, μ_p , et négativement avec la variance de celui-ci, soit σ_p^2 . Cette relation rendement – risque peut être décrite par une fonction d’utilité de la forme U(μ_p;σ_p^2). Utilisant l’approche de Guo (2003), le problème du producteur de soja peut être revu de la façon suivante :
Sous forme matricielle le rendement du prix du soja est obtenu comme suit : r_t=X_(t-1)^’ R_t
R_t représente le vecteur contenant les variations des prix anticipés du soja sur le marché à terme, et les rendements du prix du baril de pétrole.
X_(t-1)^’ représente le vecteur contenant les ratios associés aux variations des prix anticipés et aux rendements du prix du baril de pétrole.
Notre problème de maximisation est le suivant :
〖MAX〗_h { E(〖dspot〗_t⁄I_(t-1) )-1/2 λVar(〖dspot〗_t⁄I_(t-1) ) }
=〖MAX〗_h { E(〖dspot〗_t⁄I_(t-1) )-1/2 λX_(t-1)^’ (Ω_t⁄I_(t-1) ) X_(t-1) }
s/c h≤1
où I_(t-1) est l’information disponible au temps t-1 et la matrice de variance covariance conditionnelle Ω_t⁄I_(t-1) =Σ_t.
Au lieu de résoudre le problème standard de maximisation d’utilité Guo (2003) et Valiani Shohreh (2004) se concentre sur la minimisation du risque du portefeuille sujet aux fluctuations du marché. La raison pour laquelle ils abordent ainsi ce problème est que les contrats à terme ont un faible pouvoir prédictif sur les rendements espérés conditionnels ce qui conduit à des solutions optimales instables. Guo (2003) justifie cette vision alternative en supposant que les taux à terme sont des martingales ,c’est-à-dire que E(d 〖logfuture〗_t⁄I_(t-1) )=0
Notre problème de minimisation devient le suivant :
〖MIN〗_h { Var(〖dspot〗_t⁄I_(t-1) ) } =〖MIN〗_h {X_(t-1)^’ (Ω_t⁄I_(t-1) ) X_(t-1)}
s/c h≤1
2-Spécification économétrique
Soit le vecteur composé des rendements des prix « future » et des rendements du prix de baril de pétrole R_t=(d〖logfuture〗_t ,〖dlogpetrol〗_t)
Nous posons un processus VAR-GARCH qui se caractérise comme suit :
r_(t )=μ+∑_(i=1)^p▒α 〖r_(t-i)〗^’+ε_t
Avec 〖E(ε〗_t)=0, 〖Var(ε〗_t)=σ^2 I et 〖Var(ε〗_t∕I_(t-1))=H_t , H_t étant la matrice de variance covariance
Supposons que les rendements du prix de baril de pétrole sont imputés de leur moyenne et que les rendements des prix anticipés du soja en sont de même :
Soit : r_(t )=〖r_(t )〗^’-μ
En admettant la normalité conditionnelle de ceux-ci, nous avons r_t∕I_(t-1)∼N(0,H_t)
On peut à la manière de Bollerslev (1990) décomposer cette matrice en une matrice diagonale et une matrice de corrélation :
H_t=D_t R_t D_t avec D_t=diag(√(h_it ))
R_t est la matrice de corrélation conditionnelle variant dans le temps
D_t est une matrice diagonale dont les éléments sont des écarts-type variant dans le temps respectant individuellement la spécification d’un GARCH univarié
c’est-à-dire :
h_it=w_i+∑_pi▒〖α_pi 〖r²〗_(i,t-pi) 〗+∑_qi▒β_qi h_(i,t-qi)
i=1…N et ε_t=D_t^(-1) r_t avec ε_t ∼N(0,R_t)
Nous pouvons maintenant utiliser la spécification de Engle (2002) pour modéliser cette corrélation dynamique :
Q_t=(1-∑_m▒α_m^* -∑_n▒β_n^* ) Q ̅+∑_m▒α_m^* (ε_(t-m) ε_(t-m)^’ )+∑_n▒〖β_n^* Q_(t-n) 〗
R_t=Q ̃_t^(-1) Q_t Q ̃_t^(-1)
Q ̃_t est une matrice diagonale contenant les écarts-type sur la diagonale de Q_t et Q ̅ est une matrice de covariances non conditionnelle des rendements standardisés obtenu lors de la première étape d’estimation.
Cette spécification est aussi appelé modèle DCC (m, n)
Un des atouts majeurs du modèle de Engle (2002) est qu’il permet de réduire le nombre de paramètres et donc de faire des gains substantiels de temps de calcul.
Pour ce qui est de l’estimation, Engle et Sheppard (2001), ainsi que Engle (2002), utilisent comme méthode d’estimation un pseudo maximum de vraisemblance avec des écarts types robustes tout en faisant remarquer qu’il est possible d’utiliser les moindres carrés généralisés (M..M.G.).
La fonction de vraisemblance est de la forme suivante :
L=-1/2 ∑_(t=1)^T▒〖(Nlog(2π)+log|H_t |+〗 〖r_(t )〗^’ H_t^(-1) r_(t ))
=-1/2 ∑_(t=1)^T▒〖(Nlog(2π)+2log|D_t |+〗 〖r_(t )〗^’ D_t^(-1) D_t^(-1) r_(t )-ε_t ε_t^’+log|R_t |)+ε_t 〖R_t^(-1) ε〗_t^’
Cette fonction de vraisemblance, noté L(θ,φ), se décompose en un terme pour la volatilité L_v (θ) et un pour la corrélation L_c (θ,φ) et prend donc la forme :
L(θ,φ)= L_v (θ)+L_c (θ,φ)
La maximisation de cette fonction se fera en deux étapes :
Étape 1 : trouver :θ ̂ tel que θ ̂=argmax{L_v (θ)}
Dans cette première estimation, un modèle GARCH(p,q) uni-varié est appliqué à la variance conditionnelle de chaque actif. À l’issue de celle-ci, les coefficients qui expliquent la volatilité de chaque actif pris individuellement sont obtenus.
Etape 2 trouver φ tel que φ=argmax{L(θ ̂,φ)}
Dans cette seconde phase d’estimation, les coefficients des volatilités obtenues lors de la première étape, θ ̂, sont maintenues constants, et servent à conditionner la fonction de vraisemblance utilisée pour estimer les paramètres de la dynamique des corrélations, φ . Cette procédure réduit grandement le temps de calcul mais au prix d’une perte d’efficacité dans la mesure où ce n’est qu’une partie de la vraisemblance, celle des corrélations L_c (θ,φ), qui est maximisé lors de la seconde étape.
3- Estimation
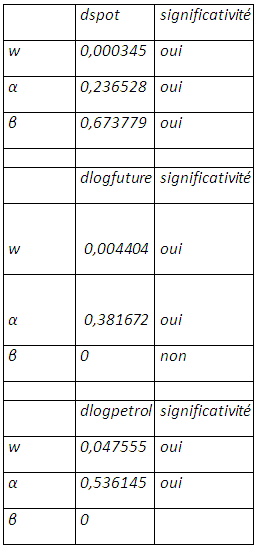
La modélisation individuelle de l’hétéroscédasticité pour chaque variable est résumée par le tableau suivant :
Notons que les rendements du prix spot du soja ont une volatilité significativement sensible aux innovations ainsi que l’effet autorégressif de la volatilité. A l’inverse, les variations des prix anticipés et prix du baril de pétrole respectent mieux une spécification arch que garch. On a une sensibilité significative aux chocs.
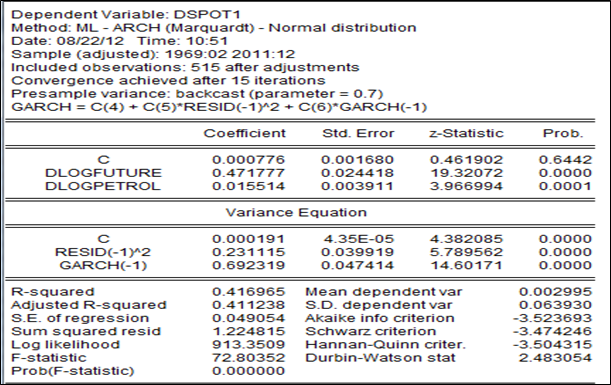
L’estimation, selon un garch(1,1) de la relation liant les variations du prix au comptant du soja à celles des prix anticipés sur le marché à terme ainsi que celles des prix du baril de pétrole, conduit à un taux de couverture de 47,17% assorti de la significativité des variables censées expliquer ces mêmes variations de prix spot du soja.les effets de chocs et de la volatilité passée sont bien significatifs.
〖dspot〗_t=c+〖hlogfuture〗_t+〖dlogpetrol〗_t
Après l’obtention des estimés des séries uni-variées, soit le vecteur de paramètre θ ̂ , nous l’utilisons pour obtenir les estimés des corrélations, ce qui correspond à la deuxième étape de Engle (2002) soit la maximisation par rapport à φ de L_c (θ ̂,φ) .
Il est obtenu :
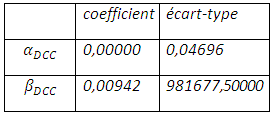
Tableau 4 : paramètres estimés de la DCC-mvgarch et leurs écart-types
Nous constatons, à l’image des variations du prix au comptant dans un cadre de corrélations conditionnelles constantes, les corrélations conditionnelles dynamiques ont un effet autorégressif plus faible à la fois pour les chocs que pour les volatilités passées. Ce comportement peut être constaté via la matrice de variance conditionnelle.
Graphe 5 : matrice des variances conditionnelles dynamiques des rendements des prix spot et à terme du soja et ceux des prix du baril de pétrole
Les variations du prix mensuel de baril de pétrole possèdent une échelle de volatilité plus grande même si le graphe laisse voire l’inverse. Les corrélations avec les volatilités des rendements des prix anticipés et prix au comptant du soja ne sont significatives que pour des variabilités vraiment amples du prix du baril de pétrole. A ce titre on peut observer les effets de la crise pétrolière de 1973, ainsi que les dernières crises financières de la dernière décennie. Une corrélation constante reste une hypothèse restrictive.
À l’aide des estimés des corrélations, nous obtenons les poids et les ratios de couverture solutions du problème de minimisation énoncé plus haut à savoir :
〖MIN〗_h { Var(〖dspot〗_t⁄I_(t-1) ) } =〖MIN〗_h {X_(t-1)^’ (Ω_t⁄I_(t-1) ) X_(t-1)}
s/c h≤1
Les taux de couverture dynamiques associés au marché à terme sont résumés par le graphique suivant :
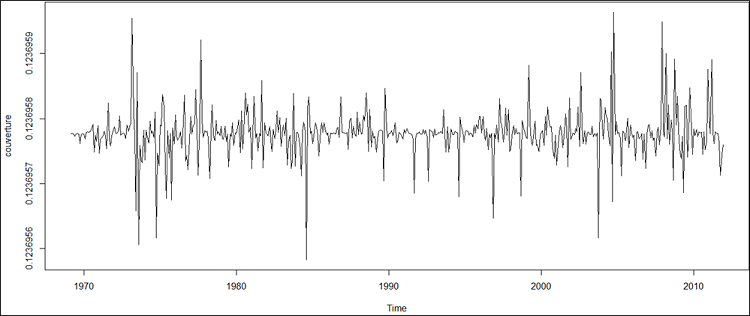
Graphe 6 : taux de couverture dynamique associés aux rendements des prix à terme
Les taux de couverture dynamiques enregistrent une moyenne de 12,37% et un écart-type de 3,623104e-08. Dans le même temps, on peut envisager un taux de couverture de 3,7% pour le prix du pétrole sous l’hypothèse forte et restrictive de la connaissance parfaite du prix.
Page suivante : Chapitre 4 : comparaison des modèles et taux de couverture
Retour au menu : La couverture des produits agricoles sur les marchés à terme : Cas du soja