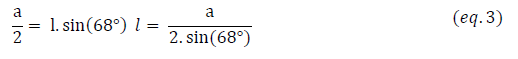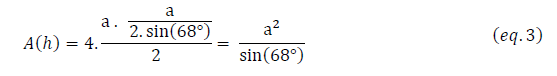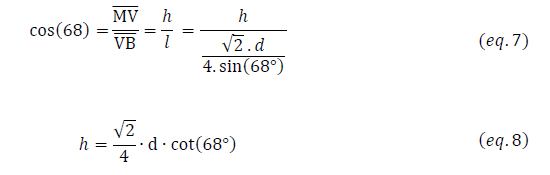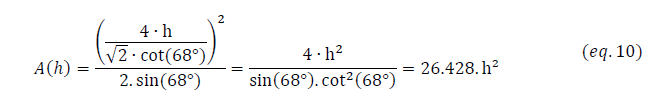1. Calcul de la fonction d’aire d’un indenteur Berkovich
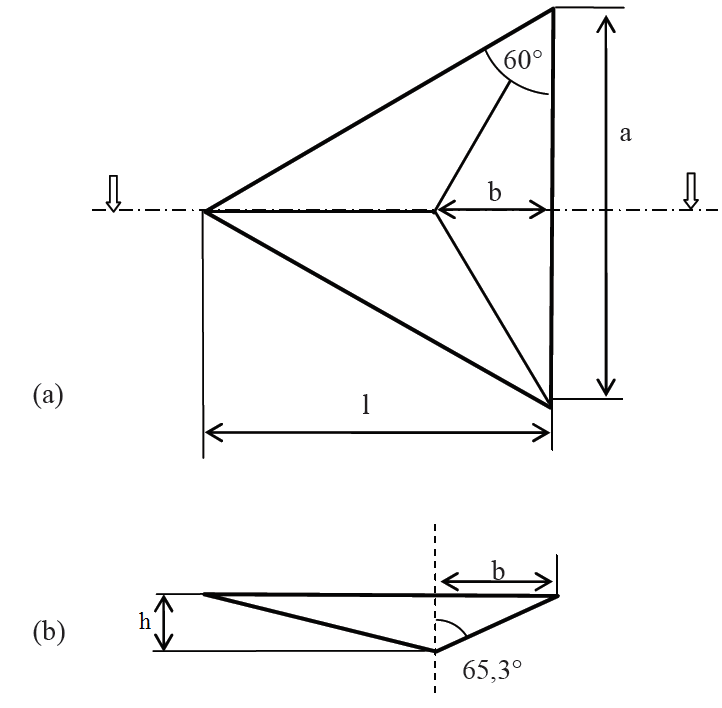
Figure A.1. Géométrie de l’indenteur Berkovich, (a) Vue de dessus, (b) vue en coupe.
L’indenteur Berkovich est une pyramide à trois faces, dont la base est un triangle équilatéral. Les faces ont une inclinaison de 65,3° par rapport à l’axe vertical. La fonction d’aire A(h) d’un indenteur Berkovich parfait, c’est-à-dire l’aire projetée en fonction de la distance h depuis la pointe, peut être calculée, géométriquement, comme suit:
La vue de dessus de l’indenteur (figure A.1.a) montre qu’il existe la relation suivante :
Ce qui donne, en remplaçant dans l’équation (1) :
La figure A.1.a montre que l’on peut également écrire :
Ce qui donne donc :
En remplaçant α dans l’équation (3) on obtient alors :
Or, la vue en coupe de l’indenteur (figure A.1.b) montre qu’il est possible de relier à suivant la relation :
Ce qui donne finalement, en substituant dans l’équation (6) :
2. Calcul de la fonction d’aire d’un indenteur Vickers
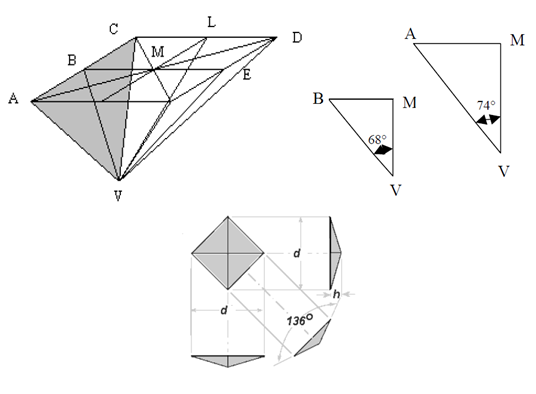
L’indenteur Vickers est une pyramide à base carrée. L’angle entre les deux faces triangulaires opposées est de 136° et entre les deux arêtes opposées est de 148° (figure A.2).
Figure A.2. Géométrie de l’indenteur Vickers.
Après la pénétration de l’indenteur à la surface d’un matériau, l’empreinte résiduelle est de forme carrée (figure A.2). L’aire réelle du contact de la pyramide avec le matériau représente quatre fois l’aire du triangle représenté en grisé sur la figure A.2. Ainsi, la fonction d’aire A(h) peut être calculée, géométriquement, comme suit:
On prendra :
La relation entre et d’après la figure A.2 peut être déterminée de la manière suivante :
Ce qui donne, en remplaçant dans la relation (eq.2) :
La figure A.2 montre que l’on peut également écrire :
Ce qui donne donc :
En remplaçant a dans l’expression (eq.3) on obtient alors :
Or, la vue en coupe de l’indenteur (figure A.2) montre qu’il est possible de relier b à d. Cette relation s’obtient de la manière suivante :
Par conséquent :
Ce qui donne finalement, en substituant d dans l’équation (2) on obtient :
Page suivante : Annexe 2. Modélisation la méthode dynamique de nanoindentation
Retour au menu : CARACTERISATION MECANIQUE ET ADHERENCE DE REVETEMENT PVD EN CARBURE DE TUNGSTENE