Dans cette partie nous chercherons à comprendre si les inondations de 2010 à Cotonou sont l’œuvre des changements climatiques ou si c’était dû aux périodes de retour.
Deux types d’inondations sont observés dans la ville de Cotonou :
– celle connue pendant la grande saison des pluies (souvent en Juin) ;
– et celle causée par le débordement du lac Nokoué (souvent en Octobre).
Ce deuxième type d’inondation nous a amené à traduire en graphes les fluctuations saisonnières de la moyenne du maximum mensuel de pluie des stations de Parakou, Savè et Bohicon ; dont les eaux alimentent le fleuve Ouémé, qui les amène au niveau du lac Nokoué à Cotonou.
Le régime hydrologique des cours d’eau dépend en premier lieu de l’altitude moyenne du bassin versant et de sa situation par rapport aux sommets. De l’analyse des graphes, il ressort que, le maximum pluviométrique mensuel est enregistré pour la plupart des cas en Juillet ou en Août.
Les fortes pluies journalières et mensuelles tombent entre Juillet, Août et Septembre, ce qui est sans doute en relation avec le régime d’écoulement des cours d’eau du Bénin qui présente un maximum entre septembre et octobre. C’est à cette période que la ville de Contonou connaît le second type d’inondation.
La comparaison des graphes montrant la variation journalière de côtes au niveau du lac Nokoué et le graphaes illustrant les fluctuations saisonnière de la moyenne du maximum mensuel de pluie , on remarque que le début de la monté du niveau de l’eau dans le lac, à l’exception de 2007 et 2009 coïncide avec les mois de fortes pluies dans les régions contributives du bassin versant de l’Ouémé (Djougou, Parakou, Savè et Bohicon).
De l’analyse des courbes illustratives des variations journalières des côtes au niveau du lac Nokoué, on constate : une croissance exponentielle du niveau de l’eau qui passe de 270cm à 380cm et 424 cm en Octobre 2010. Cette période correspond très bien au moment a lieu le deuxième type d’inondation à Cotonou, c’est dire celle d’origine fluviale.
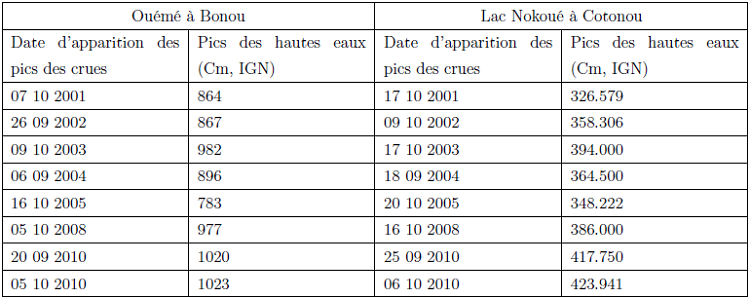
Le tableau 4.1 suivant nous permet de comprendre l’influence du débordement des eaux du fleuve Ouémé à Bonou sur le débordement des eaux du lac Nokoué à Cotonou.
Table 4.1 : Débordement à Bonou et débordement des eaux du lac Nokoué à Cotonou
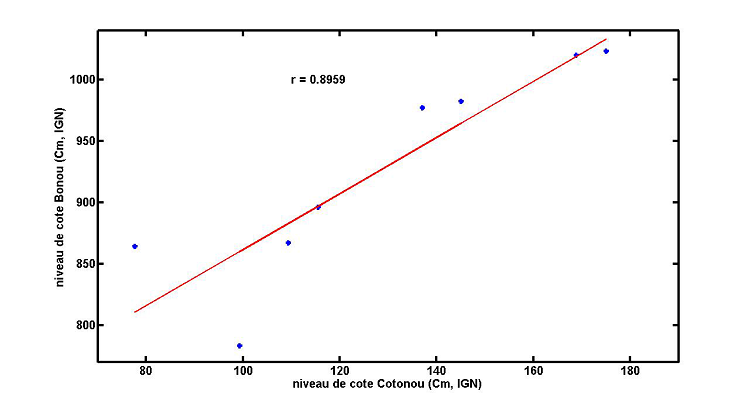
Figure 4.4 : Relation entre l’apparition des pics des hautes eaux de l’Ouémé à Bonou et le débordement des eaux du lac Nokoué à Cotonou
Dès que le niveau à l’échelle hydrométrique à Bonou atteint la cote 800 Cm IGN (Ressources en Eau), tout le delta est inondé. De l’analyse du tableau nous constatons qu’une crue constatée à Bonou prend entre cinq (5) et dix (10) jours pour survenir au niveau du lac Nokoué à Cotonou.
Aussi les débordements peuvent-ils être détournés par les défluents vers la Sô ou bien stockés dans les zones d’inondations. Toutefois, une partie des eaux peut par ailleurs être restituées au cours d’eau lors de la décrue pour les eaux stockées et lorsqu’au niveau des défluents la cote de la Sô dépasse celle de l’Ouémé, pour les eaux détournées. Selon l’importance de la crue, le sens du courant dans la Sô en amont des défluents peut alors s’inverser.
La courbe de régression ; des valeurs de cote sur l’Ouémé à Bonou et sur le Nokoué à Cotonou ; montre bien une corrélation entre les deux valeurs avec un coefficient de R² = 0; 80. Avec la figure 4.4, nous pouvons prévoir à 80% le débordement (période et intensité) des eaux du lac Nokoué à Cotonou connaissant les débordements de l’Ouémé à Bonou.
L’inodation à Cotonou, est-ce la résultante des événements pluvieux extrêmes ?
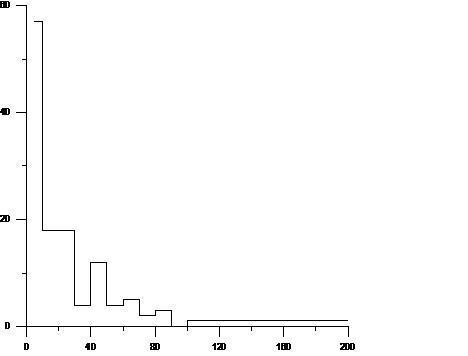
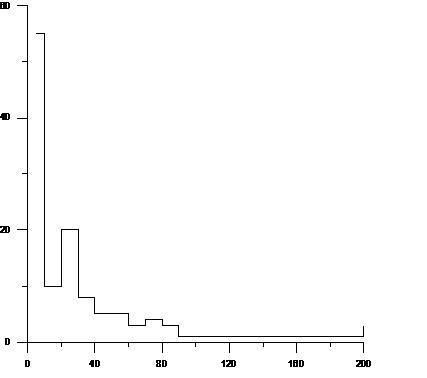
La figure 4.5 illustre le nombre événements pluvieux enrégistrés courant l’année 1962 par intervalle de volume. L’année 1962 fait partir des années exceptionnelles où la pluviométrie à dépasser les 2000 mm contre une moyenne de 1277; 05 mm (2069; 5 mm ASECNA Cotonouaéroport).
De l’analyse de ce graphe nous constatons que les événements de moins de 5mm sont les plus nombreux et qu’au fure et à mesure que le volume d’eau de pluie tombé augmente, le nombre d’événement correspondant diminue : 0 à 5 mm = 57 ; 5 à 10 mm = 18 ; 10 à 20 mm = 18 ; 20 à 30 mm = 4 ; 30 à 40 mm = 12 ; 40 à 50 mm = 4 ; 50 à 60 mm =5 ; 60 à 70 mm = 2 ; 70 à 80 mm = 3 ; 80 à 90 mm = 0 ; 90 à 100 mm = 1 ; 100 mm et plus = 1.
Figure 4.5 : Graphique illustrant le nombre d’événements pluvieux par classe de hauteur de pluie pour l’année 1962
Malgré ces 2069; 5 mm, le nombre d’événement extrême journalier est faible et égal à 1 (191; 5). Ce qui signifie que le volume d’eau recueilli et souvent conséquence des inondations n’est pas du faite des événements extrêmes mais du cumul des petits événements.
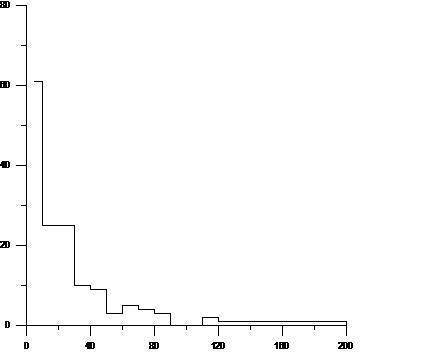
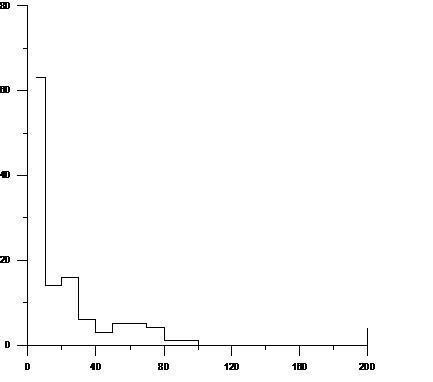
La figure 4.6 illustre le nombre événements pluvieux enrégistrés pour l’année 1968 par intervalle de volume. L’année 1968 fait partir des années exceptionnelles où la pluviométrie à dépasser les 2000 mm contre une moyenne de 1277; 05 mm. La pluviométrie totale de l’année 1968 à Cotonou est de 2470; 2 mm (ASECNA Cotonou-aéroport).
Figure 4.6 : Graphique illustrant le nombre d’événements pluvieux par classe de hauteur de pluie pour l’année 1968
Ici nous faisons la même remarque que dans le cas de la figure 4.5 : les événements de 5mm au plus sont nombreux et au fure et à mesure que le volume d’eau de pluie tombé augmente, le nombre d’événement correspondant diminue : 0 à 5 mm = 61 ; 5 à 10 mm = 25 ; 10 à 20 mm = 25 ; 20 à 30 mm = 10 ; 30 à 40 mm = 9 ; 40 à 50 mm = 3 ; 50 à 60 mm =5 ; 60 à 70 mm = 4 ; 70 à 80 mm = 3 ; 80 à 90 mm = 0 ; 90 à 100 mm = 0 ; 100 mm et plus = 3 . Les hauteurs d’eau journalières les plus élévées enrégistrées ne dépassent guère les 120 mm, la valeur la plus élevée est 119; 2 mm. Le maximum mensuel ou annuel souvent conséquence des inondations
n’est pas du faite des événements journalier exceptionels mais du cumul des événements faibles.
La figure 4.7 illustre le nombre événements pluvieux enrégistrés au de l’année 1997 par intervalle de volume. L’année 1997 fait partir des années exceptionnelles où la pluviométrie à dépasser les 2000 mm contre une moyenne de 1277; 05 mm. En 1997 il a été relevé 2203; 3 mm de pluie (ASECNA Cotonou-aéroport).
Figure 4.7 : Graphique illustrant le nombre d’événements pluvieux par classe de hauteur de pluie pour l’année 1997
De l’analyse de ce graphe nous constatons que les événements de moins de 5mm sont les plus nombreux et qu’au fure et à mesure que le volume d’eau de pluie tombé augmente, le nombre d’événement correspondant diminue : 0 à 5 mm = 55 ; 5 à 10 mm = 10 ; 10 à 20 mm = 20 ; 20 à 30 mm = 8 ; 30 à 40 mm = 5 ; 40 à 50 mm = 5 ; 50 à 60 mm = 3 ; 60 à 70 mm = 4 ; 70 à 80 mm = 3 ; 80 à 90 mm = 1 ; 90 à 100 mm = 1 ; 100 mm et plus = 3 . Malgré ces 2203; 3 mm, il n’y a qu’un seul événement de 145; 8 mm.
La figure 4.8 illustre le nombre événements pluvieux enrégistrés au de l’année 2010 par intervalle de volume. L’année 2010 fait partir des années exceptionnelles où la pluviométrie à dépasser les 2000 mm contre une moyenne de 1277; 05 mm. En 2010 la quantité totale d’eau déversée sur Cotonou est 2005; 6 mm (ASECNA Cotonou-aéroport).
Figure 4.8 : Graphique illustrant le nombre d’événements pluvieux par classe de hauteur de pluie pour l’année 2010
Même ramarque que les trois précédents graphes ; les événements de moins de 5mm sont les plus nombreux et au fure et à mesure que le volume d’eau de pluie tombé augmente, le nombre d’événement correspondant diminue : 0 à 5 mm = 57 ; 5 à 10 mm = 18 ; 10 à 20 mm = 18 ; 20 à 30 mm = 4 ; 30 à 40 mm = 12 ; 40 à 50 mm = 4 ; 50 à 60 mm = 5 ; 60 à 70 mm = 2 ; 70 à 80 mm = 3 ; 80 à 90 mm = 0 ; 90 à 100 mm = 1 ; 100 mm et plus = 1.
L’année 2010, notre année d’étude, c’est encore l’année qui a retenu toute les attentions, car pour la plupart l’inondation de 2010 est une première depuis 50 ans, pour d’autre jamais connu de mémoire d’homme.
Conclusion 1
De 1953 à 2010, c’est-à-dire que sur 58 années, quatre ont des cumuls annuel exceptionnel supérieur à 2000 mm. Parmis ces quatre années la pluviométrie de 2010 est la plus faible : 2005; 6 mm (2010) < 2069; 5mm (1962) < 2203; 3 mm (1997) < 2470; 2 mm (1968).
Ces valeurs annuelles extrêmes ne sont pas du faite des événements extrêmes, mais du cumul d’événements faibles ou moyens ayant une répartition temporelle. C’est cette répartition temporelle qui est à l’origine des mois pluvieux que nous avons (Juin et Juillet à Cotonou). Au sein de ces mois les événements pluvieux sont inégalement répartis et parfois très rapprochés (figure 4.1 et 4.2 les graphes de droite).
Ces rapprochements des événements pluvieux, couplés à la nature du sol (aquifère peu profond, sable limoneux) et le niveau piézométrique de l’eau (2; 19m de la surface du sol et moins par endroit figure 2.8), expliquent clairement l’ampleur des dégâts de 2010 et toute la mobilisation autour. L’imperméabilisation du sol par l’enfuillissement des déchets plastiques et connexes rend l’infiltration impossible, ajouté à l’évaporation très faible et la pente d’écoulement aussi faible, l’eau n’ayant pas trouvée de chemin remplira les maisons.
La pluviométrie de 2010 serait-il une conséquence des changements climatiques ou un phénomène cyclique qui était de retour ? Quelle est sa fréquence ?
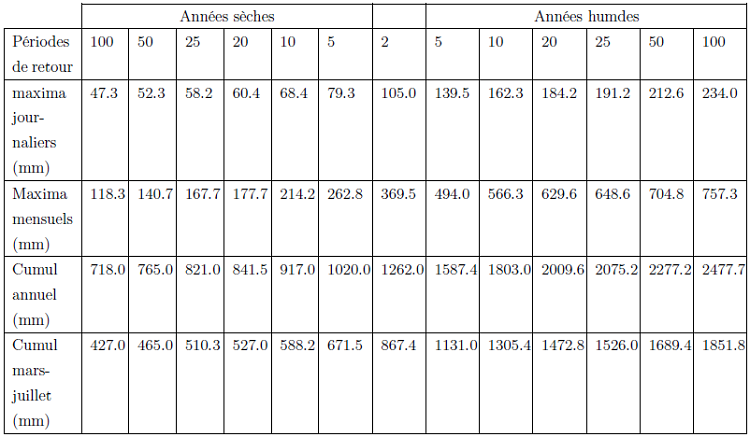
Le tableau 4.3 nous permet d’estimer les quantiles et les périodes de retour ; les graphes d’adapter l’échantillon à une loi afin de l’étudier.
Pour les maxima journaliers et mensuels les estimations sont faites en utilisant la loi de Gumbel, méthode par maximum de vraisemblance. Pour les cumuls annuels c’est la loi Normal méthode par maximum de vraisemblance qui a été utilisée pour l’estimation des quantiles et périodes de retour. Enfin, nous avons utilisé la loi des Fuites méthode par maximum de vraisemblance pour l’estimation des quantiles et périodes de retour,des cumuls de mars à juillet.
Analysons ce tableau ligne par ligne :
– maxima journaliers :
Pour une pluie de 105 mm la période de retour est de 2 ans. Pour une pluie de 139 mm sa période de retour est de 5 ans. Le maximun journalier de pluie en 2010 étant de 134; 9 mm obtenu le 03 juin, très proche de 139 mm, alors
– maxima mensuels :
Pour une pluviométrie mensuelle de 369 mm, sa période retour est de 2ans. Pour une pluviométrie mensuelle de 494 mm, sa période de retour est de 5 ans. Pour une pluviométrie mensuelle de 566 mm, sa période de retour est de 10 ans. Et pour 629 mm, sa période de retour est de 20 ans.
Le maximun pluviométrique mensuel de l’année étant de 583; 5 mm ; valeur comprise entre 566 et 629. Et puisqu’il s’agit ici d’une estimation de valeur et que le maximun mensuel de l’année 1997 étant de 622; 2 mm, valeur également comprise entre 566 et 629 nous pouvons penser à un phénomène de retour étant donné qu’entre 1997 et 2010, 13 années se sont écoulées.
– Maxima annuel :
Pour une pluviométrie annuelle de 1261 mm, sa période retour est de 2ans. Pour une pluviométrie annuelle de 1587 mm, sa période de retour est de 5 ans. Pour une pluviométrie annuelle de 1802 mm, sa période de retour est de 10 ans. Et pour 2009 mm, sa période de retour est de 20 ans.
La pluviométrie de l’année 2010 est de 2005; 6 mm une valeur très proche de 2009 dont la période de retour est comprise entre 10 et 20 ans.
– Cumul mars à juillet :
En 2010 ce cumul correspond à 1327; 3 mm ; valeur très de 1305 mm estimée dans le tableau et dont la période de retour est de 10 ans.
En dehors du maximun journalier de 2010, dont la période de retour correspond à 5ans, la période de retour de toutes les autres valeurs est légèrement supérieure ou égale à 10 ans. De ces analyses nous retenons que la pluviométrie de 2010 n’est pas un événement nouveau, mais un phénomène exceptionnel avec une de retour compris entre 15 et 30 ans. Ce qui rejoint la publication de P. OZER et al. en 2010.
Par contre, le pic de 1023 cm IGN à Bonou n’a jamais été atteint depuis 1952 (données DGEau). Puisque ce pic a d’influence sur la variation des cotes dans le Nokoué à Cotonou nous avons supposé aussi que le pic de 423; 94 cm IGN n’a jamais été atteint depuis 1952(voir tableau en annexe). Ceci pourrait être aux conditions naturelles du milieu (bassin de l’Ouémé) complètement dégradées (déforestation, érosion, exploitation minière), la quantité d’eau venant des régions contributives du bassin versant de l’Ouémé (Djougou, Parakou, Savè et dans une certaine mesure Bohicon) peut augmenter sans que la pluviométrie n’augmente dans ces régions.
Table 4.2 : Estimation des quantiles et périodes de retour des pluies
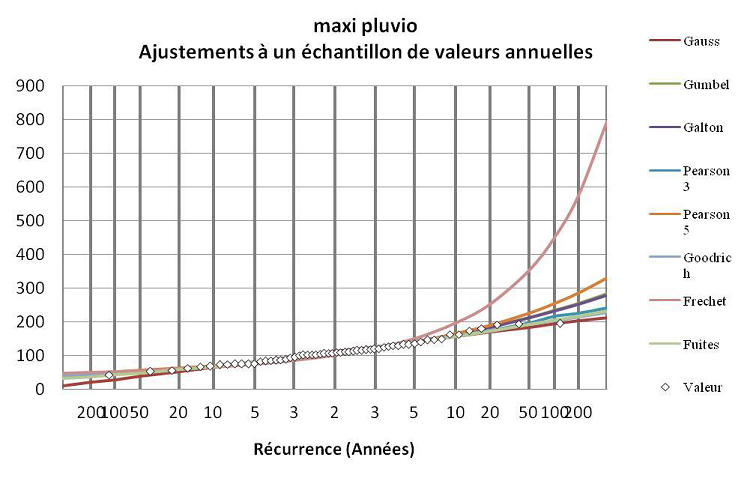
Figure 4.9 : Ajustement des maxima journaliers à Cotonou de 1953 à 2010
Cette figure montre que les valeurs sont intimement liées à quatre lois : Gauss, Fuites, Pearson3 et Gumbel. Dans la littérature (Muller 2006), en hydrologie, la loi des valeurs extrêmes la plus couramment employée en modélisation uni-variée est la loi Gumbel pour les maxima annuels. Nous pouvons alors conclure que l’échantillon s’adapte à la loi de Gumbel.
Loi : GUMBEL Méthode : Maximum de vraisemblance
Valeur des paramètres
93:775
30:441
Résultats des tests d’adéquation.
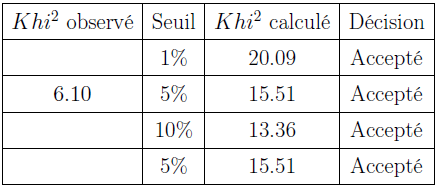
Test du Khi²
Nombre de degrés de liberté : 8:0
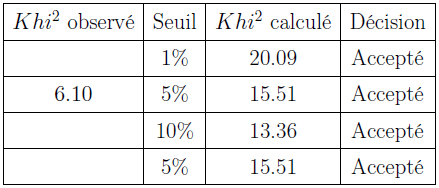
Table 4.3 : Résultat test de Khi²
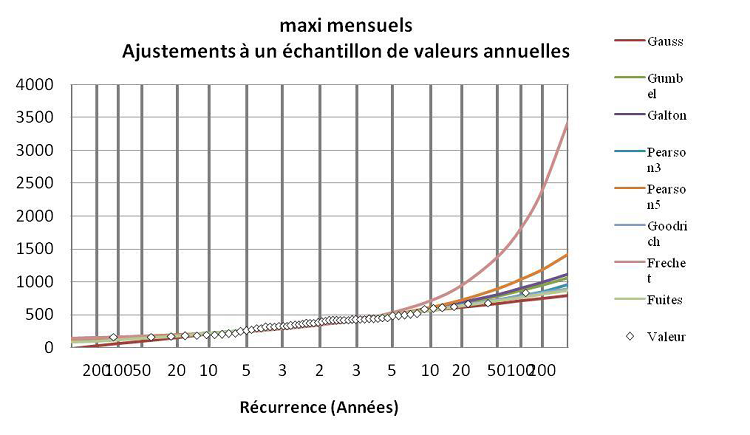
Figure 4.10 : Ajustement des maxima mensuels à Cotonou de 1953 à 2010
Cette figure montre que les valeurs sont intimement liées à quatre lois : Gauss, Fuites, Pearson3 et Gumbel. Dans la littérature (Muller 2006); en hydrologie, la loi des valeurs extrêmes la plus couramment employée en modélisation uni-variée est la loi Gumbel pour les maxima annuels. Mais pour cet échantillon le test de Khi2 est refusé et accepté pour la loi des Fuites.
Nous pouvons alors conclure que l’échantillon s’adapte à la loi des Fuites.
Loi : FUITES Méthode : Maximum de vraisemblance
Valeur des paramètres
15:219
25:105
Test du Khi²
Nombre de degrés de liberté : 8:0
Table 4.4 : Résultat test de Khi²
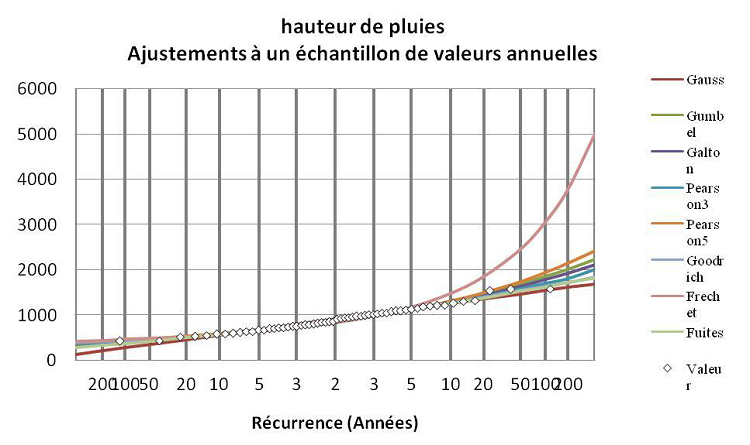
L’analyse du graphique nous permet de retenir trois lois, à savoir la loi de Gauss ou loi Normale, la loi de Gumbel, la loi Pearson3 ou loi Gama à 3 paramètres et la de Fuites. L’échantillon est adapté à la loi de Gumbel.
Loi : GUMBEL Méthode : Maximum de vraisemblance
Valeur des paramètres
782:113
232:522
Test duKhi²
Nombre de degrés de liberté : 8:0
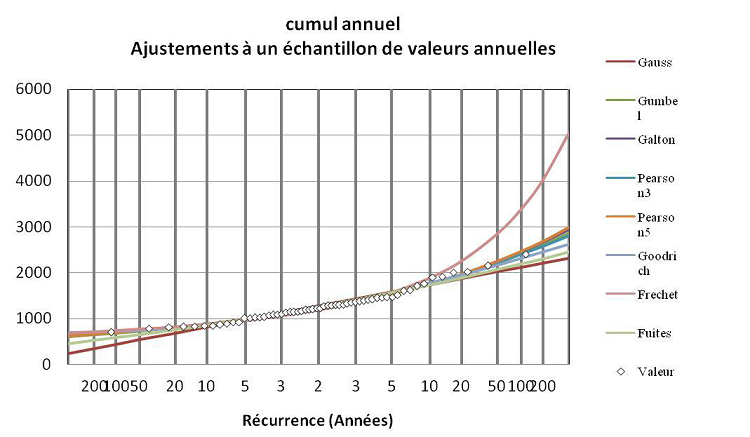
L’analyse du graphique nous permet de retenir trois lois, à savoir la loi de Gauss ou loi Normale, la loi Person3 ou loi Gama à 3 paramètres et la de Fuites. Ici nous sommes en présence des cumuls annuels à Cotonou. L’échantillon est adapté à la loi de Gauss ou loi Normale.
Loi : NORMALE Méthode : Maximum de vraisemblance
Valeur des paramètres
1322:329
368:344
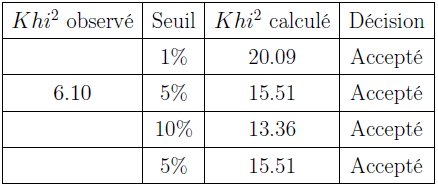
Test du Khi²
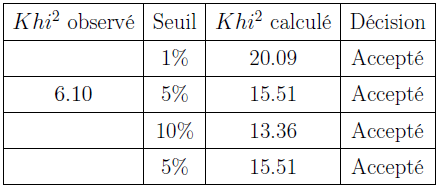
Figure 4.11 : Ajustement des pluies de mars à juillet de 1953 à 2010
Table 4.5 : Résultat test de Khi²
Figure 4.12 : Ajustement des cumuls annuels de 1953 à 2010
Nombre de degrés de liberté : 8:0
Table 4.6 : Résultat test de Khi2
Conclusion 2
Après ces résultats, il serait trop tôt de lier le phénomène pluviométrique de 2010 à Cotonou à un quelconque changement climatique. Surtout que de nos le milieu naturelle a subi une énorme transformation (occupation anarchique des terres et exutoires naturels de l’eau, encombrement des cours d’eau, exploitation forestière et minière).
L’hypothèse de phénomène cyclique avec un temps de retour est très probable. Vue le rapprochement du maximun mensuel de 2010 à celui de 1997 et ceci dans le même mois, on a tendance à penser à un retour des événements 13 ans après. Mais la différence entre le cumul annuel de 1997 et celui de 2010 est trop grande (200 mm), nous ne pouvons donc pas certifier le retour des événements de 1997.