Plusieurs contributions sur la relation inflation et croissance , incluant celle de Khan et Senhadji (2000) , Druckker , Gomis-Porqueras et Hernandez-Verme (2005) ,Yasir Mubarick (2005) ont utilisé le modèle de seuil en panel initié par Hansen(1999). En s’inspirant de l’étude de Kahn et Senhadji(2000) qui a permis d’évaluer avec robustesse l’intervalle de 7 à 11% de seuil d’inflation pour les pays en developpement, Mubarick (2005) a déterminé le seuil d’inflation de la Jordanie qui s’établirait selon ces estimations à 9%. Ainsi notre étude s’inspirant de celle Kahn et Senhadji (2000) s’appuie sur le modèle de seuil de Hansen.
Utilisant les données en panel , cette méthodologie nous permet d’appréhender non seulement un effet de seuil mais aussi de pouvoir évaluer celui-ci dans le cadre de la zone UEMOA. La caractéristique essentielle du modèle de Hansen (1999) est qu’il permet d’estimer le seuil et non de l’imposer.
En effet, les modèles de panel à seuil non dynamiques (par opposition à ceux qui font intervenir des variables endogènes retardées) ont été développés à l’origine par Hansen (1999). L’introduction de cette nouvelle classe de modèles avait pour objectif de décrire le lien non linéaire entre le comportement d’investissement des firmes et les contraintes financières qu’elles subissent. Un modèle de panel à seuil avec effets décrivant la relation entre l’inflation et la croissance économique et possédant une unique fonction de transition admet l’écriture générale suivante :
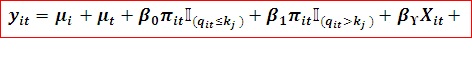 Avec Yit la variable expliquée (le taux de croissance économique), πit la principale variable explicative (le taux d’inflation), Xit les variables de contrôle, µi l’effet fixe et µt l’effet aléatoire; Et où la fonction de transition est représentée par une fonction indicatrice Π qui prend la valeur 1 si la contrainte entre parenthèses est respectée, 0 sinon. Hansen (1999) impose deux restrictions sur cette spécification : la variable explicative et la variable de transition doivent nécessairement varier avec le temps, et les résidus sont supposés iid (6) avec une moyenne nulle et une variance finie.
Avec Yit la variable expliquée (le taux de croissance économique), πit la principale variable explicative (le taux d’inflation), Xit les variables de contrôle, µi l’effet fixe et µt l’effet aléatoire; Et où la fonction de transition est représentée par une fonction indicatrice Π qui prend la valeur 1 si la contrainte entre parenthèses est respectée, 0 sinon. Hansen (1999) impose deux restrictions sur cette spécification : la variable explicative et la variable de transition doivent nécessairement varier avec le temps, et les résidus sont supposés iid (6) avec une moyenne nulle et une variance finie.
L’originalité de ce modèle réside dans la représentation d’un panel en plusieurs régimes distincts, caractérisés chacun par une dynamique linéaire. La transition est brutale sachant qu’un pays peut basculer d’un régime à l’autre en une période. Mais, contrairement aux modèles avec ruptures déterministes, le passage d’un régime à l’autre n’est ni définitif, ni daté. La transition est gouvernée par la comparaison des écarts de valeur entre un seuil et une variable de transition.
Par ailleurs, les données de panel présentent des avantages qui permettent de cerner avec précision l’expression des données à notre disposition. Une de ses caractéristiques fondamentales est leur double dimension(les différents pays et le temps). Cette double dimension, généralement individuelle et temporelle permet d’étudier simultanément la dynamique et l’hétérogénéité des comportements des agents (Nerlove et balestra, 1995). L’analyse en donnée de panel nous permet de recueillir un nombre élevé d’observations et de prendre en compte l’hétérogénéité des économies de l’UEMOA et les caractéristiques non observables.
Les observations individuelles sont réparties entre les deux régimes. Leur appartenance à l’un ou à l’autre dépend de la position de la variable de saut par rapport au seuil. On distingue les différents régimes suivant la valeur de leur pente :
β0 si qit< k ou β1 si qit >k. Si nous considérons uniquement deux régimes, la valeur du seuil doit être recherchée parmi les valeurs de la variable de transition .
Dans le cadre de notre étude, nous nous appuyons sur l’étude effectuée par Kahn et Senhadji pour supposer qu’en tant que pays en développement, le seuil de l’inflation dans la zone UEMOA est compris entre 7 et 11%. Ce sont donc ses valeurs de notre variable de transition à savoir 7%,8%,9%,10% et 11% que nous allons examiner pour évaluer le seuil de l’inflation.
6 iid : indépendamment et identiquement distribué
Page suivante : 4.2. Données et variables
Retour au menu : Analyse de la relation inflation et croissance économique dans les pays de l’UEMOA
