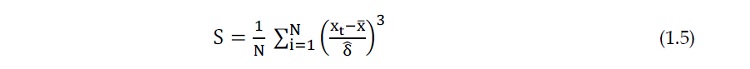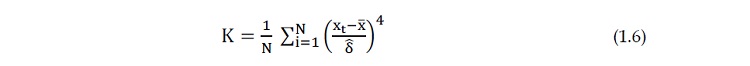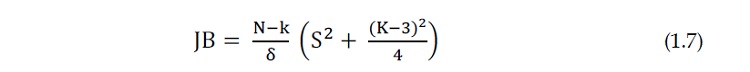L’analyse de la statistique descriptive consiste à évaluer le Skewness qui est un
indicateur d’asymétrie, calculer le Kurtosis qui présente un coefficient d’aplatissement et
d’effectuer l’essai de Jarque-Bera qui présente un test de normalité.
3.2.1.1. Le Skewness :
C’est un outil statistique qui mesure le degré d’asymétrie de la distribution soit le
moment d’ordre 3, il est définit par :
(1.5)
Où :
N : Le nombre d’observations,
xt : L’observation à l’instant (t),
x¯ : La moyenne des observations,
d : L’estimateur de l’écart-type.
Trois cas sont à envisager :
? S > 0 : La distribution est asymétrique vers la droite.
? S =0 : La distribution est qualifiée de normale et symétrique.
? S < 0 : La distribution est asymétrique vers la gauche.
3.2.1.2. Le Kurtosis :
C’est un coefficient qui mesure le degré d’aplatissement de la distribution soit le
moment d’ordre 4, il est donné par l’équation suivante :
(1.6)
Trois cas sont à envisager :
? K > 3 : La distribution est dite pointue et donc leptokurtotique.
? K = 3 : La distribution est qualifiée de normale.
? K< 3 : La distribution est dite écrasée et donc playkurtotique.
3.2.1.3. Le test de Jarque-Bera :
C’est un test qui regroupe les deux coefficients mentionnés ci-dessus par la mesure
de leur différence d’une série par rapport à ceux d’une distribution normale. Il permet de
tester la normalité d’une distribution et il est calculé comme suit :
(1.7)
Où :
? K : Le nombre de variables explicatives(ou le nombre de coefficients estimés).
Donc l’hypothèse de normalité des résidus au seuil a est rejetée.
3.2.1.4. Statistiques descriptives des séries des prix et des dividendes
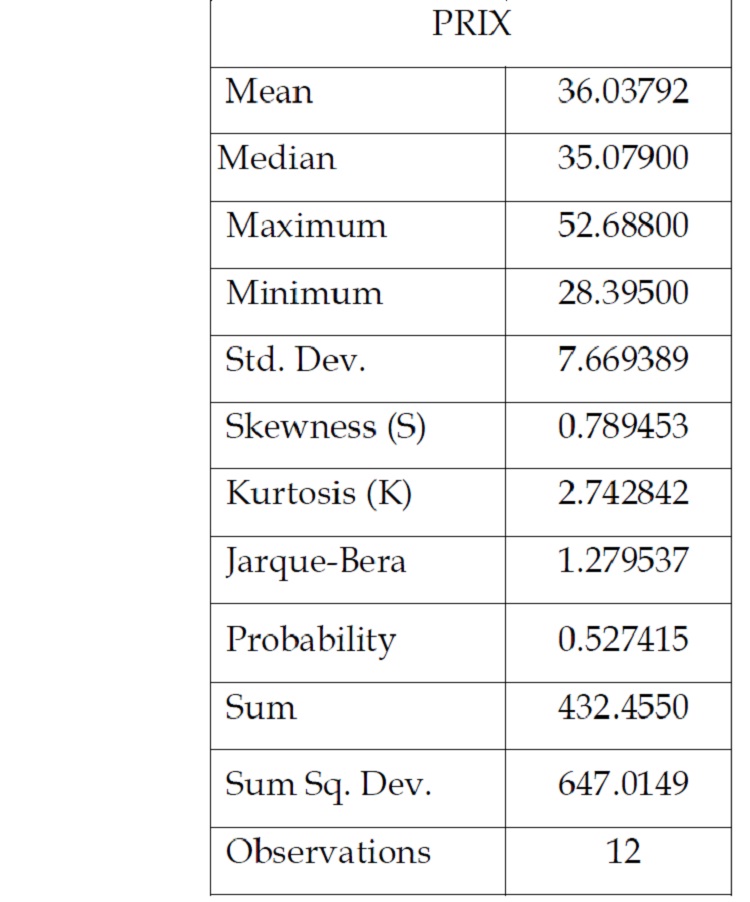
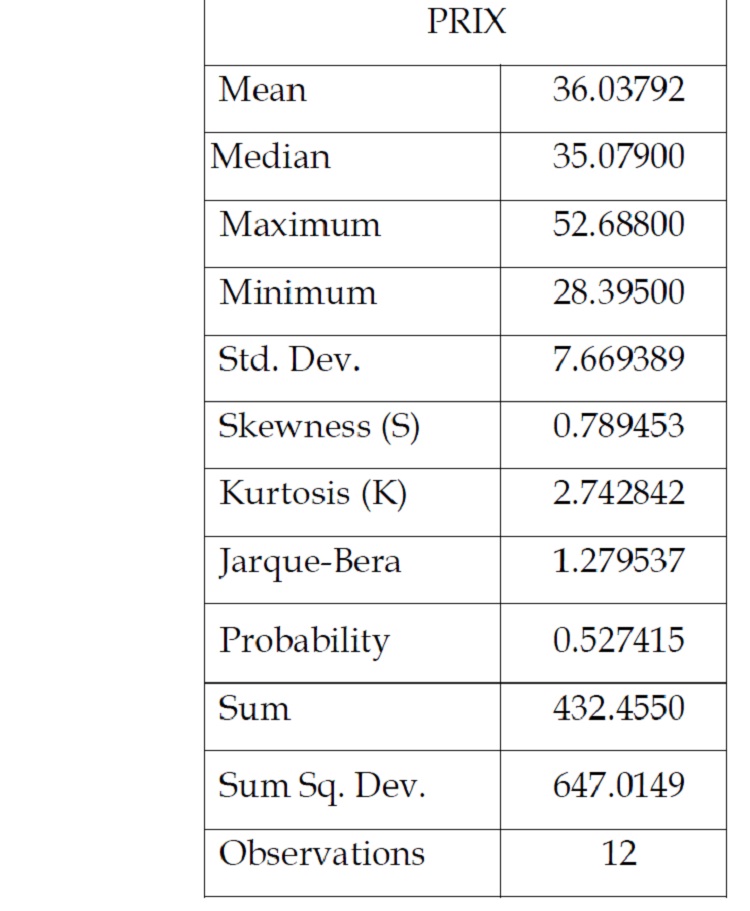
Tableau 1 .1 : Statistiques descriptives de la série des prix
D’après le tableau 1.1 nous pouvons remarquer que
la distribution de la série des prix est significativement
différente de la distribution normale au seuil de 1%. En
effet, la série des prix est caractérisée par un coefficient
d’asymétrie (S) égal à (0.789453) qui est supérieur à 0
donc une asymétrie vers la droite et par un coefficient
d’aplatissement (K) égal à (2.742842) qui est inférieur à
3 et donc la distribution de la série des prix est
playkurtotique. La statistique de Jarque –Bera est
supérieure à ???(2) lu dans la table (probabilité
critique égal à (0.527415)) donc l’hypothèse de
normalité de la série des prix est rejetée.
Tableau 1.2 : Statistiques descriptives de la série des dividendes
A partir du tableau 1.2 nous pouvons constater que
la distribution de la série des dividendes est
significativement différente de la distribution normale au
seuil de 1%, et ce parce qu’elle est caractérisée par un
coefficient d’asymétrie (S) égal à (-2.218016) qui est
inférieur à 0 donc une asymétrie vers la gauche et par un
coefficient d’aplatissement (K) égal à (7.304470) qui est
largement supérieur à 3 et donc la distribution de la série
des dividendes est leptokurtotique. La statistique de
Jarque –Bera est largement supérieure à ???(2) lu dans la
table (probabilité critique égal à (0.000071)) donc
l’hypothèse de normalité de la série des dividendes est
rejetée.