Dans ce travail, C’est le test de Dickey Fuller augmenté (DFA) (voir tableau 1 annexe 1) qui est utilisé pour vérifier la stationnarité des séries. Ainsi que celui de Phillipe-Perron (tableau 2 annexe 1).
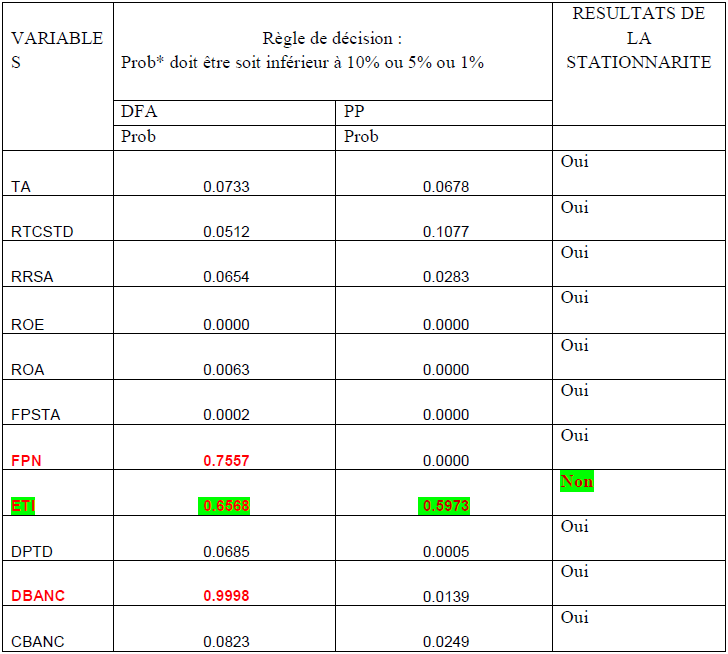
Tableau 5 : les résultats du test de stationnarité de DFA et Phillips Perron
Source : Auteur : à partir de STATA, *= probabilité
Lorsque la valeur de la probabilité d’une variable est inférieure soit à 10%, 5%, 1% alors la variable est stationnaire, au cas contraire on accepte l’hypothèse de non stationnarité de la variable.
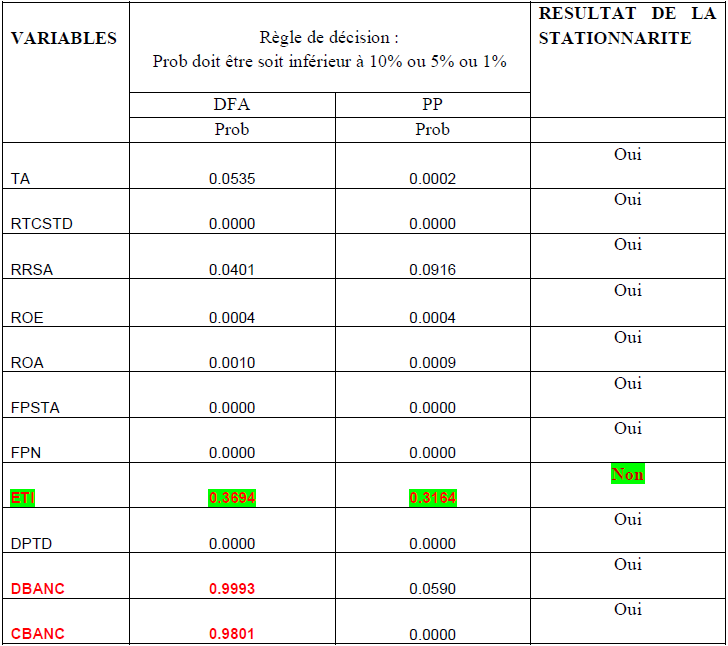
Tableau 6 : les résultats du test de stationnarité de DFA et Phillips Perron avec trend
Source : Auteur : à partir de STATA
Ces tests sont faits pour les raisons de non stationnarité de trois de nos variables : ETI, DBANC, CBANC. Ces variables restent toujours non stationnaires, d’où le test de stationnarité de DFA et PP avec trend et constante.
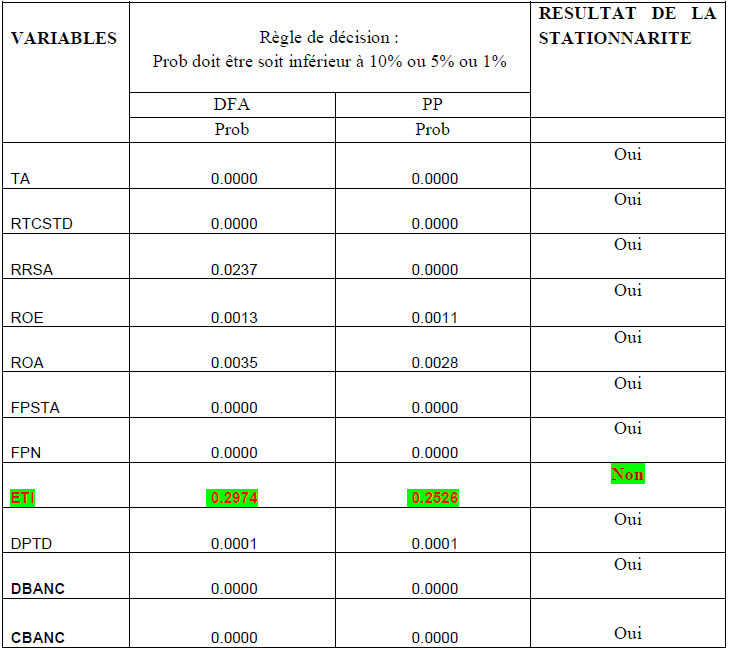
Tableau 7 : les résultats du test de stationnarité de DFA et Phillips Perron avec trend et constante
Source : auteur, à partir de STATA
Ces tableaux permettent de faire ressortir les variables stationnaires avec le test de DFA et PP à niveau c’est-à-dire cointégrées (voir annexe 1). Au regard des tableaux ci-dessus, on peut constater que toutes nos variables sont stationnaires dans le test de DFA et PP avec trend et constante sauf la variable ETI. Cette variable sera éliminée lors de l’estimation du modèle bien qu’elle soit stationnaire en différence première aussi bien avec DFA qu’avec Pillips Perron.
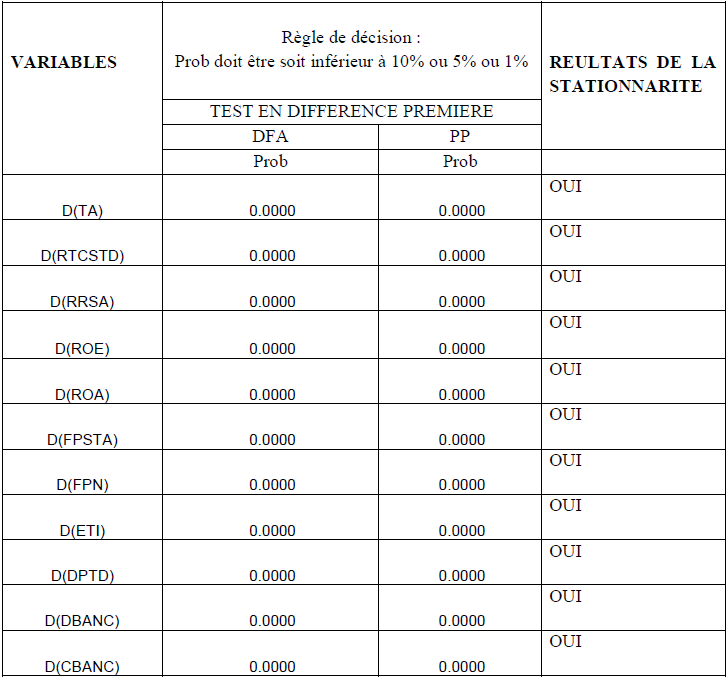
Tableau 8 : les résultats du test de stationnarité de DFA et Phillips Perron en différence première
Source : auteur, à partir de STATA
On peut constater que toutes nos variables sont stationnaires en différence première avec le test de DFA et celui de PP.
La régression par la méthode des moindres carrés ordinaires permet de vérifier la présence de l’auto corrélation des résidus et de l’hétéroscédasticité.
– Test D’autocorrelation de Breusch-Godfrey (BG)
L’autocorrelation des résidus rend caduque les commentaires sur la validité des modèles ou des tests statistiques, il convient de tester l’autocorrelation des erreurs par le test de BG. Les résultats montrent qu’il y a autocorrélation (voir tableau 1 annexe 2).
– Test d’hétéroscédasticité
Les résultats de ce teste présenté dans le tableau 1 en annexe 2 montre que le modèle est hétéroscédastique. D’où la correction de l’hétéroscédasticité dans nos différents modèles.
La présence de l’autocorrélation et de l’hétéroscédasticité nous permet d’utiliser les méthodes des moindres carrés généralisés (MCG) pour estimer nos deux modèles de régression. Mais avant il est nécessaire de procéder à la correction de l’hétéroscédasticité. Cette correction se fait par la procédure de White. Le résultat de cette correction se trouve dans le tableau 1 de l’annexe 2 et dans le tableau 1 de l’annexe 3.
Page suivante : V.2- ESTIMATION DES MODELES PAR LES MCG
Retour au menu : ACTIVITE D’OCTROI DE CREDIT ET RENTABILITE DES BANQUES COMMERCIALES AU CAMEROUN