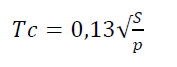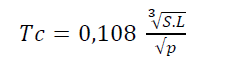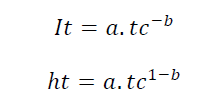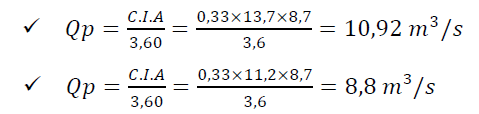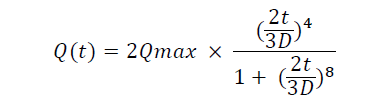Compte tenu de l’objet de l’étude, l’analyse hydrologique a pour buts de déterminer les débits caractéristiques des crues de l’Henx et les volumes d’apports correspondants. Ces caractéristiques hydrologiques ont été estimées au droit du site potentiel envisagé pour créer un bassin écrêteur sur l’Henx à l’amont de la RD 31.
La détermination du débit maximum probable de crues est obtenu par la méthode du GRADEX à raccordement progressif à partir du débit décennal (Q10) et pour une pluie d’occurrence centennale prise égale à P100 = 2 × P10 (cf. 4.1.2.1)
4.1.1 Estimation de Q10
Le débit maximal instantané d’occurrence décennale Q10 a été estimé par la méthode du Temps de Concentration, à partir des caractéristiques géomorphologiques du bassin versant et des caractéristiques pluviométriques statistiques communiquées par Météo France pour le poste de Pau Uzein.
4.1.1.1 Le temps de concentration – méthodes de calculs
Le temps de concentration est défini comme le temps nécessaire à une particule d’eau pour parcourir le plus long chemin hydraulique depuis la limite du bassin jusqu’à l’exutoire.
De nombreuses formules permettent de calculer le temps de concentration sur un bassin versant. A chacune de ces formules sont applicables un domaine de validité, que ce soit pour la taille des bassins versants étudiés ou pour les résultats obtenus. Sachant qu’il n’existe pas une seule formule qui aurait été construite pour le bassin versant de l’Henx, nous avons confronté 3 formules différentes de temps de concentration qui sont les suivantes :
a) VENTURA (Ray) :
. Tc = temps de concentration en heures
. S = surface du bassin versant en km² (8,7 km²)
. p = Pente en m/m (0,007 m/m)
Domaine de validité compris entre 1 et 20 km² ou supérieur à 10 km² selon les ouvrages.
b) TURRAZA :
. Tc = temps de concentration en minutes
. S = surface du bassin versant en hectares (870 hectares)
. L = cheminement hydraulique le plus long en mètres (6 700 m)
. p = pente en m/m (0,007 m/m)
c) Ven Te CHOW :
. Tc = temps de concentration en minutes
. L = cheminement hydraulique le plus long en mètres (6 700 m)
. p = pente en m/m (0,007 m/m)
Domaine de validité pour les bassins versants agricoles de 1 à 2 hectares.
Nota : Il est compliqué de trouver le domaine de validité des formules de temps de concentrations, d’autant plus que selon les littératures, pour une même formule, les temps de validité varient.
4.1.1.2 Temps de concentration – Résultats
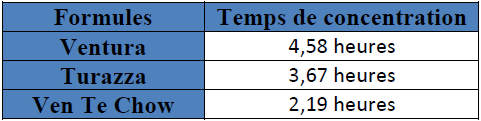
Tableau 3 : Comparaison de 3 formules de temps de concentration
Compte tenu des incertitudes attachées à l’hydrologie en l’absence de mesures hydrométriques exploitables, deux temps de concentration ont été retenus afin d’en mesurer l’incidence sur les débits et les volumes de crues. Les temps de concentration retenus sont 2,8 heures et 3,8 heures.
Il n’existe pas une formule de temps de concentration propre au bassin versant de l’Henx. De plus nous savons que les formules destinées aux bassins versants importants ont tendance à surestimer les temps de concentration.
Et à l’inverse les formules destinées aux petits bassins versants ont tendance à sous-estimer les temps de concentration pour les petits bassins. C’est pourquoi nous utilisons plusieurs formules afin d’avoir un ordre d’idée du temps de concentration.
Les temps de concentration choisis sont issus de l’expérience acquise au cours des années d’études réalisées par l’ingénieur responsable du projet.
Le choix de deux temps de concentration différents va permettre de pouvoir comparer hydrauliquement leurs conséquences afin d’établir l’ouvrage écrêteur en fonction du temps de concentration le plus contraignant.
4.1.1.3 Intensité de la pluie – Formule de MONTANA
La formule de MONTANA décrit la relation existant entre l’intensité, la durée et la fréquence des pluies mais également entre la hauteur, la durée et la fréquence des pluies. Elle s’exprime de la manière suivante :
. It = Intensité durant le temps t en mm/min (ou mm/heure)
. tc = durée de la pluie équivalente au temps de concentration (en minutes ou en heures)
. ht = Hauteur des précipitations en mm
. a et b = coefficients de MONTANA
Nota = les coefficients de MONTANA varient selon les régions et la période de retour. Ici a = 8,814 et b = 0,713 pour une période de retour de 10 ans et une durée de pluie allant de 2 à 24 heures.
Les intensités calculées pour une pluie décennale sont donc les suivantes :
– 13,7 mm/h pour un temps de concentration de 2,8 heures
– 11,2 mm/h pour un temps de concentration de 3,8 heures
4.1.1.4 Calcul du débit décennal – Q10
Le débit de pointe peut être évalué en utilisant la méthode rationnelle. Celle-ci est bien adaptée aux bassins versants de moins de 250 ha et dont la pente longitudinale moyenne est supérieure à 0,5 %.
La méthode rationnelle est basée sur l’hypothèse d’un évènement pluvieux constant et uniforme sur l’ensemble d’un bassin versant. Elle suppose également l’homogénéité spatiale du bassin versant (extrapolation du coefficient de ruissellement à l’ensemble de la surface). Enfin, nous posons comme dernière hypothèse que l’ensemble des pluies ruisselées arrivent au même moment à l’exutoire, engendrant un débit de crue maximum.
. Qp = débit de pointe en m3/s
. C = Coefficient de ruissellement (0,33)
. I = Intensité de l’averse en mm/h est uniforme dans le temps et dans l’espace sur l’ensemble du bassin drainé (13,7 mm/h et 11,2 mm/h)
. A = aire du bassin versant en km² (8,7 km²)
Soit un débit décennal de 10,92 m³/s et 8,8 m³/s respectivement pour des temps de concentration de 2,8 heures et 3,8 heures. Cependant, si le débit engendré par un même bassin versant est plus fort pour un faible temps de concentration, c’est une relation inverse qui se produit lorsqu’on parle des volumes générés. Sur un temps de concentration important, logiquement, les volumes produits seront plus importants (Cf 4.1.3.1)
On note à ce stade de l’étude qu’un temps de concentration plus faible engendre une intensité de débits plus forts.
4.1.1.5 Synthèse partielle de données n°1
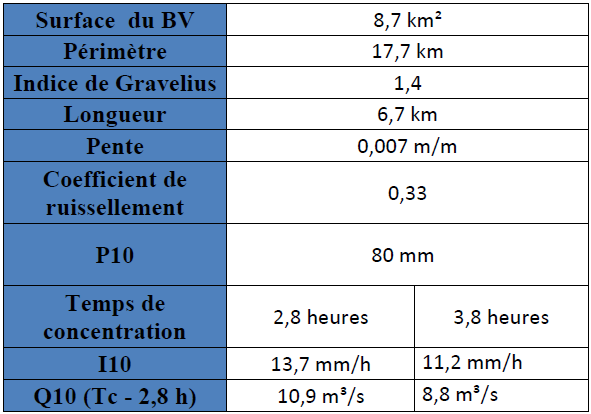
L’ensemble des données énumérées et calculées dans les points précédents sont synthétisés dans le tableau suivant :
Tableau 4 : Synthèse de données n°1
4.1.2 Estimation des débits de crues exceptionnelles par la méthode du GRADEX
4.1.2.1 Principe
L’Henx et son bassin versant, n’ont jamais fait l’objet de mesures précises, que ce soit pour des mesures de débits ou météorologiques. En hydrologie comme dans tous les domaines le manque de données pousse à établir des astuces permettant de palier à ce problème. La méthode du GRADEX en est une. Cette méthode graphique permet de calculer un gradient des valeurs extrêmes, d’où le nom qui lui est attribuée : GRADEX. La méthode du GRADEX a été développée à l’origine par des ingénieurs d’EDF (Guillot, Duband, 1967).
Le GRADEX s’effectue essentiellement en quatres étapes successives :
– Le calcul du GRADEX des pluies (nécessaire pour le calcul de l’étape suivante)
– Le calcul du GRADEX des débits (nécessaire pour le calcul de l’étape suivante)
– Le calcul du GRADEX par la méthode sécuritaire (utilité graphique)
– Le calcul du GRADEX par méthode à raccordement progressif – appelée également raccordement esthétique (Utilité Graphique)
Pour l’Henx les débits maximaux instantanés des crues d’occurrence rares 20, 30, 50 et 100 ans et plus sont calculés grâce à cette méthode, à partir du débit Q10 et pour une pluie d’occurrence centennale prise égale à P100 = 2 × P10. N’ayant pas 100 ans de relevés pluviométriques à notre disposition, nous assimilons la pluie de référence à une pluie centennale. A Pau, cette pluie de référence est égale à P100 = 2 × P10.
L’ensemble des résultats qui vont suivre sont synthétisés la synthèse partielle n°2 (Cf. 4.1.2.6)
4.1.2.2 Estimation du GRADEX des pluies de Durée Gp(D)
4.1.2.3 Raccordement du GRADEX des pluies en GRADEX des débits :
4.1.2.4 Méthode sécuritaire
Lorsque la méthode du GRADEX a été développée dans les années 70, les ingénieurs Guillot et Duband ont émis l’hypothèse qu’au-delà d’une pluie décennale, toute l’eau tombée sur la surface du sol ruisselait et était donc transformée en débit.
4.1.2.5 GRADEX à raccordement progressif (esthétique)
En émettant l’hypothèse que, dès la pluie décennale, toute la pluie ruisselée est transformée en débit, Guillot et Duband ont omis que certains phénomènes de stockages entrent en jeu, ayant pour effet de surestimer l’effet d’une pluie sur une crue. D’où le nom qui a été attribué à cette méthode « sécuritaire ». La méthode du raccordement progressif prend en compte les phénomènes de stockages.
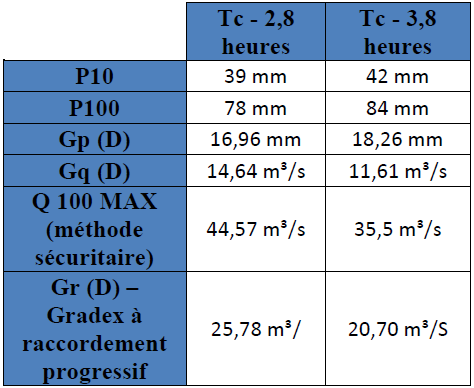
4.1.2.6 Synthèse partielle de données n°2
Tableau 5 : Synthèse de données n°2
4.1.2.7 Réalisation Graphique sur papier Gumbel
En statistique, des évènements « normaux » comme la taille d’une population ou son âge sont représentés par une Loi de Gauss (Loi Normale). Les évènements extrêmes comme les pluies ou les débits vicennaux, centennaux, etc… dépendent d’une Loi de Gumbel représentée par une asymptote à décroissance asymptotiquement exponentielle. Un papier de Gumbel, présente 4 axes et 4 échelles différentes d’où la possibilité d’obtenir le type de courbe citée précédemment.
Théoriquement, sur ce papier sont placés l’ensemble des données de pluviométrie et de débits qui ont été relevés. N’ayant aucun de ces relevés HEA a tracée ces graphiques en appliquant la méthode suivante :
Exemple pour un temps de concentration de 2,8 heures :
– Tracé du GRADEX des pluies :
a) Placer le point P2. P2 (en mm) est calculé avec la formule de Montana et a pour valeur 26 mm ;
b) Placer P10, qui ici, prend la valeur 39 mm ;
c) Relier P2 à P10 pour obtenir la courbe de tendance des pluies d’occurrence 2 à 10 ans ;
d) Placet le point P100 = 2 X P10 et relier P10 à P100. On obtient le GRADEX des pluies, autrement dit, la courbe de tendance des pluies d’occurrence 10 à 100 ans.
– Estimation des débits extrêmes par la méthode sécuritaire :
e) Placer le point Q2 = Q10/2 ;
f) Placer Q10 calculé dans le paragraphe 2.1.1.1.4, égal 10,9 m³/sec ;
g) Relier Q2 à Q10. Le point Q10 est appelé « valeur pivot »
h) Placer le point Q100, calculé avec la méthode sécuritaire (Cf. 4.1.2.4)
i) Placer les points Q20, Q50, Q100 (Cf. 4.1.2.5) et Q500 calculés avec la méthode estéthique
j) Relier ces points pour tracer la courbe du GRADEX à raccordement progressif
On s’aperçoit que Q100 de la méthode sécuritaire est largement supérieur à Q100 de la méthode du GRADEX progressif.
Cf – Annexe n°3 – 2,8 h
Cf – Annexe n° 4 – 3,8 h
Nota : les échelles des axes des pluies et débits doivent être ajustées l’une en fonction de l’autre avec d’avoir un ensemble visuellement cohérent.
4.1.3 Estimation des volumes caractéristiques des crues
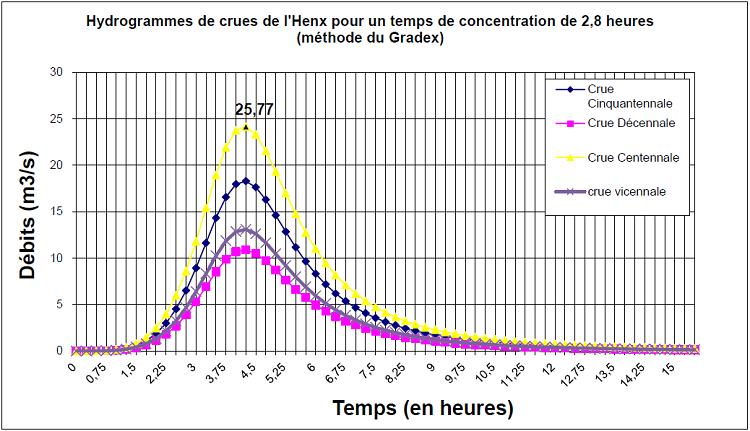
Afin de pouvoir connaitre au mieux les volumes que l’ouvrage écrêteur de crue devra stocker, nous devons dans un premier temps calculer le volume qu’une crue centennale génère. Pour cela, nous traçons les hydrogrammes de crue pour des temps de concentration de 2,8 heures et 3,8 heures. Ces hydrogrammes sont calculés et tracés pour des crues décennales, vicennales, cinquantenales et centennales. Les hydrogrammes de crue sont calculés au moyen de la formule suivante établie par L’IRSTEA de Lyon (anciennement CEMAGREF) :
Avec :
. t = temps en heure
. D = temps de concentration en heure
Les hydrogrammes obtenus sont les suivants :
Figure 11 : Hydrogrammes de crues de l’Henx pour un temps de concentration de 2,8 heures
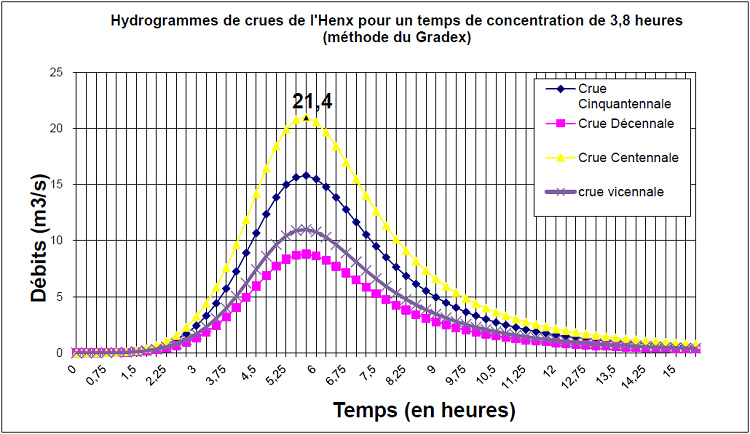
Figure 12 : Hydrogrammes de crues de l’Henx pour un temps de concentration de 3,8 heures
4.1.3.1 Estimation des volumes de crues et des volumes à stocker :
La formule d’IRSTEA permet de calculer des débits au pas de temps désiré, il est donc aisé d’obtenir le volume généré par une crue.
Il faut également mettre les volumes pour Q10, Q20, Q50, Q100
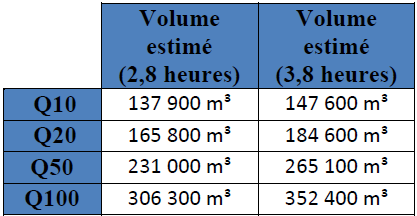
Volumes générés :
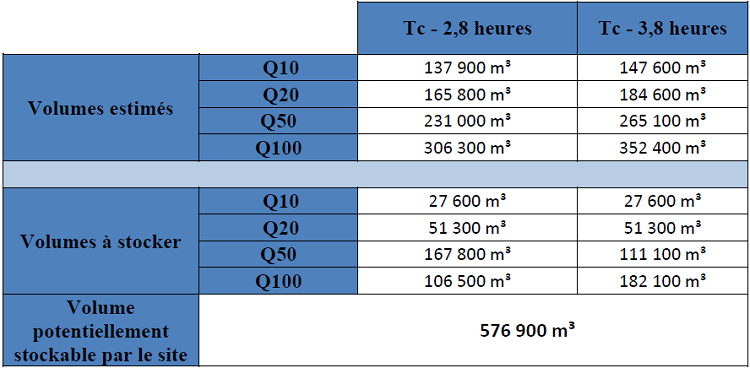
Tableau 6 : Estimation des volumes produits en fonction des types de crues
Le débit de plein bord étant de 5 m³/sec, pour connaître le volume à stocker, il suffit de déduite au volume estimé généré, le volume généré par un débit de 5m³/sec sur le pas de temps durant lequel le débit de la crue est supérieur à 5m³/sec (Cf. hydrogrammes – 4.1.3).
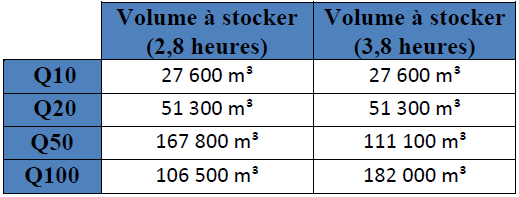
Volumes de crues à stocker :
Tableau 7 : Estimation des volumes à stocker en fonction des types de crues
4.1.4 Estimation du volume potentiellement stockable par le site
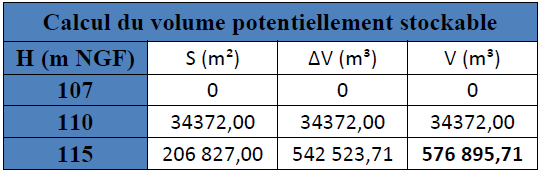
Suite à l’étude de la carte IGN (échelle 1/25 000) de la commune de Mont nous pouvons estimer grâce aux courbes altimétriques le volume d’eau que peut stocker le site en considérant un barrage d’une hauteur maximale de 8 mètres. Le tableau ci-après récapitule les volumes approximatifs stockables le site en fonction de la cote NGF et de la hauteur de stockage.
Tableau 8 : Calcul du volume stockable par le site
. S = surface du site à la côte NGF correspondante, en m²
. ΔV = variation du volume en m3
. V = volume stockable à la côte NGF correspondante
Ces volumes appellent les remarques suivantes :
. Compte tenu des contraintes foncières, la hauteur utile de l’ouvrage sera limitée pour le site à une hauteur de 7-8 mètres environ au maximum, soit un volume stockable de l’ordre de 576 900 m³ ;
. En comparaison des volumes de crues exceptionnelles estimées (Cf. 4.1.3.1), ces volumes potentiels sont très significatifs et devraient donc permettre de laminer efficacement les débits maximaux instantanés de ces crues.
4.1.4.1 Synthèse partielle de données n°3
Tableau 9 : Synthèse de données n°3
Page suivante : PARTIE V : SYNTHESE ET CRITIQUES
Retour au menu : Etude Hydraulique préalable à la conception d’un ouvrage écrêteur de crue